Vectors and Matrices¶

The functions described in this chapter provide a simple vector and matrix interface to ordinary C arrays. The memory management of these arrays is implemented using a single underlying type, known as a block. By writing your functions in terms of vectors and matrices you can pass a single structure containing both data and dimensions as an argument without needing additional function parameters. The structures are compatible with the vector and matrix formats used by BLAS routines.

Data types¶

All the functions are available for each of the standard data-types. The versions for double have the prefix gsl_block, gsl_vector and gsl_matrix. Similarly the versions for single-precision float arrays have the prefix gsl_block_float, gsl_vector_float and gsl_matrix_float. The full list of available types is given below,

Prefix	Type
gsl_block	double
gsl_block_float	float
gsl_block_long_double	long double
gsl_block_int	int
gsl_block_uint	unsigned int
gsl_block_long	long
gsl_block_ulong	unsigned long
gsl_block_short	short
gsl_block_ushort	unsigned short
gsl_block_char	char
gsl_block_uchar	unsigned char
gsl_block_complex	complex double
gsl_block_complex_float	complex float
gsl_block_complex_long_double	complex long double

Corresponding types exist for the gsl_vector and gsl_matrix functions.

Blocks¶

For consistency all memory is allocated through a gsl_block structure. The structure contains two components, the size of an area of memory and a pointer to the memory. The gsl_block structure looks like this,

type gsl_block¶

typedef struct
{
  size_t size;
  double * data;
} gsl_block;

Vectors and matrices are made by slicing an underlying block. A slice is a set of elements formed from an initial offset and a combination of indices and step-sizes. In the case of a matrix the step-size for the column index represents the row-length. The step-size for a vector is known as the stride.

The functions for allocating and deallocating blocks are defined in gsl_block.h.

Block allocation¶

The functions for allocating memory to a block follow the style of malloc and free. In addition they also perform their own error checking. If there is insufficient memory available to allocate a block then the functions call the GSL error handler (with an error number of GSL_ENOMEM) in addition to returning a null pointer. Thus if you use the library error handler to abort your program then it isn’t necessary to check every alloc.

gsl_block *gsl_block_alloc(size_t n)¶

This function allocates memory for a block of n double-precision elements, returning a pointer to the block struct. The block is not initialized and so the values of its elements are undefined. Use the function gsl_block_calloc() if you want to ensure that all the elements are initialized to zero.

Zero-sized requests are valid and return a non-null result. A null pointer is returned if insufficient memory is available to create the block.

gsl_block *gsl_block_calloc(size_t n)¶: This function allocates memory for a block and initializes all the elements of the block to zero.

void gsl_block_free(gsl_block *b)¶: This function frees the memory used by a block b previously allocated with gsl_block_alloc() or gsl_block_calloc().

Reading and writing blocks¶

The library provides functions for reading and writing blocks to a file as binary data or formatted text.

int gsl_block_fwrite(FILE *stream, const gsl_block *b)¶: This function writes the elements of the block b to the stream stream in binary format. The return value is 0 for success and GSL_EFAILED if there was a problem writing to the file. Since the data is written in the native binary format it may not be portable between different architectures.

int gsl_block_fread(FILE *stream, gsl_block *b)¶: This function reads into the block b from the open stream stream in binary format. The block b must be preallocated with the correct length since the function uses the size of b to determine how many bytes to read. The return value is 0 for success and GSL_EFAILED if there was a problem reading from the file. The data is assumed to have been written in the native binary format on the same architecture.

int gsl_block_fprintf(FILE *stream, const gsl_block *b, const char *format)¶: This function writes the elements of the block b line-by-line to the stream stream using the format specifier format, which should be one of the %g, %e or %f formats for floating point numbers and %d for integers. The function returns 0 for success and GSL_EFAILED if there was a problem writing to the file.

int gsl_block_fscanf(FILE *stream, gsl_block *b)¶: This function reads formatted data from the stream stream into the block b. The block b must be preallocated with the correct length since the function uses the size of b to determine how many numbers to read. The function returns 0 for success and GSL_EFAILED if there was a problem reading from the file.

Example programs for blocks¶

The following program shows how to allocate a block,

#include <stdio.h>
#include <gsl/gsl_block.h>

int
main (void)
{
  gsl_block * b = gsl_block_alloc (100);

  printf ("length of block = %zu\n", b->size);
  printf ("block data address = %p\n", b->data);

  gsl_block_free (b);
  return 0;
}

Here is the output from the program,

length of block = 100
block data address = 0x804b0d8

Vectors¶

Vectors are defined by a gsl_vector structure which describes a slice of a block. Different vectors can be created which point to the same block. A vector slice is a set of equally-spaced elements of an area of memory.

The gsl_vector structure contains five components, the size, the stride, a pointer to the memory where the elements are stored, data, a pointer to the block owned by the vector, block, if any, and an ownership flag, owner. The structure is very simple and looks like this,

type gsl_vector¶

typedef struct
{
  size_t size;
  size_t stride;
  double * data;
  gsl_block * block;
  int owner;
} gsl_vector;

The size is simply the number of vector elements. The range of valid indices runs from 0 to size-1. The stride is the step-size from one element to the next in physical memory, measured in units of the appropriate datatype. The pointer data gives the location of the first element of the vector in memory. The pointer block stores the location of the memory block in which the vector elements are located (if any). If the vector owns this block then the owner field is set to one and the block will be deallocated when the vector is freed. If the vector points to a block owned by another object then the owner field is zero and any underlying block will not be deallocated with the vector.

The functions for allocating and accessing vectors are defined in gsl_vector.h.

Vector allocation¶

The functions for allocating memory to a vector follow the style of malloc and free. In addition they also perform their own error checking. If there is insufficient memory available to allocate a vector then the functions call the GSL error handler (with an error number of GSL_ENOMEM) in addition to returning a null pointer. Thus if you use the library error handler to abort your program then it isn’t necessary to check every alloc.

gsl_vector *gsl_vector_alloc(size_t n)¶: This function creates a vector of length n, returning a pointer to a newly initialized vector struct. A new block is allocated for the elements of the vector, and stored in the block component of the vector struct. The block is “owned” by the vector, and will be deallocated when the vector is deallocated. Zero-sized requests are valid and return a non-null result.

gsl_vector *gsl_vector_calloc(size_t n)¶: This function allocates memory for a vector of length n and initializes all the elements of the vector to zero.

void gsl_vector_free(gsl_vector *v)¶: This function frees a previously allocated vector v. If the vector was created using gsl_vector_alloc() then the block underlying the vector will also be deallocated. If the vector has been created from another object then the memory is still owned by that object and will not be deallocated.

Accessing vector elements¶

Unlike Fortran compilers, C compilers do not usually provide support for range checking of vectors and matrices. 1 The functions gsl_vector_get() and gsl_vector_set() can perform portable range checking for you and report an error if you attempt to access elements outside the allowed range.

The functions for accessing the elements of a vector or matrix are defined in gsl_vector.h and declared extern inline to eliminate function-call overhead. You must compile your program with the preprocessor macro HAVE_INLINE defined to use these functions.

GSL_RANGE_CHECK_OFF¶: If necessary you can turn off range checking completely without modifying any source files by recompiling your program with the preprocessor definition GSL_RANGE_CHECK_OFF. Provided your compiler supports inline functions the effect of turning off range checking is to replace calls to gsl_vector_get(v,i) by v->data[i*v->stride] and calls to gsl_vector_set(v,i,x) by v->data[i*v->stride]=x. Thus there should be no performance penalty for using the range checking functions when range checking is turned off.

GSL_C99_INLINE¶: If you use a C99 compiler which requires inline functions in header files to be declared inline instead of extern inline, define the macro GSL_C99_INLINE (see Inline functions). With GCC this is selected automatically when compiling in C99 mode (-std=c99).

int gsl_check_range¶: If inline functions are not used, calls to the functions gsl_vector_get() and gsl_vector_set() will link to the compiled versions of these functions in the library itself. The range checking in these functions is controlled by the global integer variable gsl_check_range. It is enabled by default—to disable it, set gsl_check_range to zero. Due to function-call overhead, there is less benefit in disabling range checking here than for inline functions.

double gsl_vector_get(const gsl_vector *v, const size_t i)¶: This function returns the i-th element of a vector v. If i lies outside the allowed range of 0 to size - 1 then the error handler is invoked and 0 is returned. An inline version of this function is used when HAVE_INLINE is defined.

void gsl_vector_set(gsl_vector *v, const size_t i, double x)¶: This function sets the value of the i-th element of a vector v to x. If i lies outside the allowed range of 0 to size - 1 then the error handler is invoked. An inline version of this function is used when HAVE_INLINE is defined.

double *gsl_vector_ptr(gsl_vector *v, size_t i)¶
const double *gsl_vector_const_ptr(const gsl_vector *v, size_t i)¶: These functions return a pointer to the i-th element of a vector v. If i lies outside the allowed range of 0 to size - 1 then the error handler is invoked and a null pointer is returned. Inline versions of these functions are used when HAVE_INLINE is defined.

Initializing vector elements¶

void gsl_vector_set_all(gsl_vector *v, double x)¶: This function sets all the elements of the vector v to the value x.

void gsl_vector_set_zero(gsl_vector *v)¶: This function sets all the elements of the vector v to zero.

int gsl_vector_set_basis(gsl_vector *v, size_t i)¶: This function makes a basis vector by setting all the elements of the vector v to zero except for the i-th element which is set to one.

Reading and writing vectors¶

The library provides functions for reading and writing vectors to a file as binary data or formatted text.

int gsl_vector_fwrite(FILE *stream, const gsl_vector *v)¶: This function writes the elements of the vector v to the stream stream in binary format. The return value is 0 for success and GSL_EFAILED if there was a problem writing to the file. Since the data is written in the native binary format it may not be portable between different architectures.

int gsl_vector_fread(FILE *stream, gsl_vector *v)¶: This function reads into the vector v from the open stream stream in binary format. The vector v must be preallocated with the correct length since the function uses the size of v to determine how many bytes to read. The return value is 0 for success and GSL_EFAILED if there was a problem reading from the file. The data is assumed to have been written in the native binary format on the same architecture.

int gsl_vector_fprintf(FILE *stream, const gsl_vector *v, const char *format)¶: This function writes the elements of the vector v line-by-line to the stream stream using the format specifier format, which should be one of the %g, %e or %f formats for floating point numbers and %d for integers. The function returns 0 for success and GSL_EFAILED if there was a problem writing to the file.

int gsl_vector_fscanf(FILE *stream, gsl_vector *v)¶: This function reads formatted data from the stream stream into the vector v. The vector v must be preallocated with the correct length since the function uses the size of v to determine how many numbers to read. The function returns 0 for success and GSL_EFAILED if there was a problem reading from the file.

Vector views¶

In addition to creating vectors from slices of blocks it is also possible to slice vectors and create vector views. For example, a subvector of another vector can be described with a view, or two views can be made which provide access to the even and odd elements of a vector.

type gsl_vector_view¶

type gsl_vector_const_view¶

A vector view is a temporary object, stored on the stack, which can be used to operate on a subset of vector elements. Vector views can be defined for both constant and non-constant vectors, using separate types that preserve constness. A vector view has the type gsl_vector_view and a constant vector view has the type gsl_vector_const_view. In both cases the elements of the view can be accessed as a gsl_vector using the vector component of the view object. A pointer to a vector of type gsl_vector * or const gsl_vector * can be obtained by taking the address of this component with the & operator.

When using this pointer it is important to ensure that the view itself remains in scope—the simplest way to do so is by always writing the pointer as &view.vector, and never storing this value in another variable.

gsl_vector_view gsl_vector_subvector(gsl_vector *v, size_t offset, size_t n)¶

gsl_vector_const_view gsl_vector_const_subvector(const gsl_vector *v, size_t offset, size_t n)¶

These functions return a vector view of a subvector of another vector v. The start of the new vector is offset by offset elements from the start of the original vector. The new vector has n elements. Mathematically, the i-th element of the new vector v' is given by:

v'(i) = v->data[(offset + i)*v->stride]

where the index i runs from 0 to n - 1.

The data pointer of the returned vector struct is set to null if the combined parameters (offset, n) overrun the end of the original vector.

The new vector is only a view of the block underlying the original vector, v. The block containing the elements of v is not owned by the new vector. When the view goes out of scope the original vector v and its block will continue to exist. The original memory can only be deallocated by freeing the original vector. Of course, the original vector should not be deallocated while the view is still in use.

The function gsl_vector_const_subvector() is equivalent to gsl_vector_subvector() but can be used for vectors which are declared const.

gsl_vector_view gsl_vector_subvector_with_stride(gsl_vector *v, size_t offset, size_t stride, size_t n)¶

gsl_vector_const_view gsl_vector_const_subvector_with_stride(const gsl_vector *v, size_t offset, size_t stride, size_t n)¶

These functions return a vector view of a subvector of another vector v with an additional stride argument. The subvector is formed in the same way as for gsl_vector_subvector() but the new vector has n elements with a step-size of stride from one element to the next in the original vector. Mathematically, the i-th element of the new vector v' is given by:

v'(i) = v->data[(offset + i*stride)*v->stride]

where the index i runs from 0 to n - 1.

Note that subvector views give direct access to the underlying elements of the original vector. For example, the following code will zero the even elements of the vector v of length n, while leaving the odd elements untouched:

gsl_vector_view v_even = gsl_vector_subvector_with_stride (v, 0, 2, n/2);
gsl_vector_set_zero (&v_even.vector);

A vector view can be passed to any subroutine which takes a vector argument just as a directly allocated vector would be, using &view.vector. For example, the following code computes the norm of the odd elements of v using the BLAS routine dnrm2:

gsl_vector_view v_odd = gsl_vector_subvector_with_stride (v, 1, 2, n/2);
double r = gsl_blas_dnrm2 (&v_odd.vector);

The function gsl_vector_const_subvector_with_stride() is equivalent to gsl_vector_subvector_with_stride() but can be used for vectors which are declared const.

gsl_vector_view gsl_vector_complex_real(gsl_vector_complex *v)¶

gsl_vector_const_view gsl_vector_complex_const_real(const gsl_vector_complex *v)¶

These functions return a vector view of the real parts of the complex vector v.

The function gsl_vector_complex_const_real() is equivalent to gsl_vector_complex_real() but can be used for vectors which are declared const.

gsl_vector_view gsl_vector_complex_imag(gsl_vector_complex *v)¶

gsl_vector_const_view gsl_vector_complex_const_imag(const gsl_vector_complex *v)¶

These functions return a vector view of the imaginary parts of the complex vector v.

The function gsl_vector_complex_const_imag() is equivalent to gsl_vector_complex_imag() but can be used for vectors which are declared const.

gsl_vector_view gsl_vector_view_array(double *base, size_t n)¶

gsl_vector_const_view gsl_vector_const_view_array(const double *base, size_t n)¶

These functions return a vector view of an array. The start of the new vector is given by base and has n elements. Mathematically, the i-th element of the new vector v' is given by:

v'(i) = base[i]

where the index i runs from 0 to n - 1.

The array containing the elements of v is not owned by the new vector view. When the view goes out of scope the original array will continue to exist. The original memory can only be deallocated by freeing the original pointer base. Of course, the original array should not be deallocated while the view is still in use.

The function gsl_vector_const_view_array() is equivalent to gsl_vector_view_array() but can be used for arrays which are declared const.

gsl_vector_view gsl_vector_view_array_with_stride(double *base, size_t stride, size_t n)¶

gsl_vector_const_view gsl_vector_const_view_array_with_stride(const double *base, size_t stride, size_t n)¶

These functions return a vector view of an array base with an additional stride argument. The subvector is formed in the same way as for gsl_vector_view_array() but the new vector has n elements with a step-size of stride from one element to the next in the original array. Mathematically, the i-th element of the new vector v' is given by:

v'(i) = base[i*stride]

where the index i runs from 0 to n - 1.

Note that the view gives direct access to the underlying elements of the original array. A vector view can be passed to any subroutine which takes a vector argument just as a directly allocated vector would be, using &view.vector.

The function gsl_vector_const_view_array_with_stride() is equivalent to gsl_vector_view_array_with_stride() but can be used for arrays which are declared const.

Copying vectors¶

Common operations on vectors such as addition and multiplication are available in the BLAS part of the library (see BLAS Support). However, it is useful to have a small number of utility functions which do not require the full BLAS code. The following functions fall into this category.

int gsl_vector_memcpy(gsl_vector *dest, const gsl_vector *src)¶: This function copies the elements of the vector src into the vector dest. The two vectors must have the same length.

int gsl_vector_complex_conj_memcpy(gsl_vector_complex *dest, const gsl_vector_complex *src)¶: This function copies the complex conjugate of the vector src into the vector dest. The two vectors must have the same length.

int gsl_vector_swap(gsl_vector *v, gsl_vector *w)¶: This function exchanges the elements of the vectors v and w by copying. The two vectors must have the same length.

Exchanging elements¶

The following functions can be used to exchange, or permute, the elements of a vector.

int gsl_vector_swap_elements(gsl_vector *v, size_t i, size_t j)¶: This function exchanges the i-th and j-th elements of the vector v in-place.

int gsl_vector_reverse(gsl_vector *v)¶: This function reverses the order of the elements of the vector v.

Vector operations¶

int gsl_vector_add(gsl_vector *a, const gsl_vector *b)¶: This function adds the elements of vector b to the elements of vector a. The result $a_i \leftarrow a_i + b_i$ is stored in a and b remains unchanged. The two vectors must have the same length.

int gsl_vector_sub(gsl_vector *a, const gsl_vector *b)¶: This function subtracts the elements of vector b from the elements of vector a. The result $a_i \leftarrow a_i - b_i$ is stored in a and b remains unchanged. The two vectors must have the same length.

int gsl_vector_mul(gsl_vector *a, const gsl_vector *b)¶: This function multiplies the elements of vector a by the elements of vector b. The result $a_i \leftarrow a_i * b_i$ is stored in a and b remains unchanged. The two vectors must have the same length.

int gsl_vector_div(gsl_vector *a, const gsl_vector *b)¶: This function divides the elements of vector a by the elements of vector b. The result $a_i \leftarrow a_i / b_i$ is stored in a and b remains unchanged. The two vectors must have the same length.

int gsl_vector_scale(gsl_vector *a, const double x)¶: This function multiplies the elements of vector a by the constant factor x. The result $a_i \leftarrow x a_i$ is stored in a.

int gsl_vector_add_constant(gsl_vector *a, const double x)¶: This function adds the constant value x to the elements of the vector a. The result $a_i \leftarrow a_i + x$ is stored in a.

double gsl_vector_sum(const gsl_vector *a)¶: This function returns the sum of the elements of a, defined as $\sum_{i=1}^n a_i$

int gsl_vector_axpby(const double alpha, const gsl_vector *x, const double beta, gsl_vector *y)¶: This function performs the operation $y \leftarrow \alpha x + \beta y$ . The vectors x and y must have the same length.

The following additional functions are available for complex vector operations.

int gsl_vector_complex_div_real(gsl_vector_complex *a, const gsl_vector *b)¶: This function divides the elements of complex vector a by the elements of real vector b. The result $a_i \leftarrow a_i / b_i$ is stored in a and b remains unchanged. The two vectors must have the same length.

Finding maximum and minimum elements of vectors¶

The following operations are only defined for real vectors.

double gsl_vector_max(const gsl_vector *v)¶: This function returns the maximum value in the vector v.

double gsl_vector_min(const gsl_vector *v)¶: This function returns the minimum value in the vector v.

void gsl_vector_minmax(const gsl_vector *v, double *min_out, double *max_out)¶: This function returns the minimum and maximum values in the vector v, storing them in min_out and max_out.

size_t gsl_vector_max_index(const gsl_vector *v)¶: This function returns the index of the maximum value in the vector v. When there are several equal maximum elements then the lowest index is returned.

size_t gsl_vector_min_index(const gsl_vector *v)¶: This function returns the index of the minimum value in the vector v. When there are several equal minimum elements then the lowest index is returned.

void gsl_vector_minmax_index(const gsl_vector *v, size_t *imin, size_t *imax)¶: This function returns the indices of the minimum and maximum values in the vector v, storing them in imin and imax. When there are several equal minimum or maximum elements then the lowest indices are returned.

Vector properties¶

The following functions are defined for real and complex vectors. For complex vectors both the real and imaginary parts must satisfy the conditions.

int gsl_vector_isnull(const gsl_vector *v)¶
int gsl_vector_ispos(const gsl_vector *v)¶
int gsl_vector_isneg(const gsl_vector *v)¶
int gsl_vector_isnonneg(const gsl_vector *v)¶: These functions return 1 if all the elements of the vector v are zero, strictly positive, strictly negative, or non-negative respectively, and 0 otherwise.

int gsl_vector_equal(const gsl_vector *u, const gsl_vector *v)¶: This function returns 1 if the vectors u and v are equal (by comparison of element values) and 0 otherwise.

Example programs for vectors¶

This program shows how to allocate, initialize and read from a vector using the functions gsl_vector_alloc(), gsl_vector_set() and gsl_vector_get().

#include <stdio.h>
#include <gsl/gsl_vector.h>

int
main (void)
{
  int i;
  gsl_vector * v = gsl_vector_alloc (3);

  for (i = 0; i < 3; i++)
    {
      gsl_vector_set (v, i, 1.23 + i);
    }

  for (i = 0; i < 100; i++) /* OUT OF RANGE ERROR */
    {
      printf ("v_%d = %g\n", i, gsl_vector_get (v, i));
    }

  gsl_vector_free (v);
  return 0;
}

Here is the output from the program. The final loop attempts to read outside the range of the vector v, and the error is trapped by the range-checking code in gsl_vector_get().

$ ./a.out
v_0 = 1.23
v_1 = 2.23
v_2 = 3.23
gsl: vector_source.c:12: ERROR: index out of range
Default GSL error handler invoked.
Aborted (core dumped)

The next program shows how to write a vector to a file.

#include <stdio.h>
#include <gsl/gsl_vector.h>

int
main (void)
{
  int i;
  gsl_vector * v = gsl_vector_alloc (100);

  for (i = 0; i < 100; i++)
    {
      gsl_vector_set (v, i, 1.23 + i);
    }

  {
     FILE * f = fopen ("test.dat", "w");
     gsl_vector_fprintf (f, v, "%.5g");
     fclose (f);
  }

  gsl_vector_free (v);
  return 0;
}

After running this program the file test.dat should contain the elements of v, written using the format specifier %.5g. The vector could then be read back in using the function gsl_vector_fscanf (f, v) as follows:

#include <stdio.h>
#include <gsl/gsl_vector.h>

int
main (void)
{
  int i;
  gsl_vector * v = gsl_vector_alloc (10);

  {
     FILE * f = fopen ("test.dat", "r");
     gsl_vector_fscanf (f, v);
     fclose (f);
  }

  for (i = 0; i < 10; i++)
    {
      printf ("%g\n", gsl_vector_get(v, i));
    }

  gsl_vector_free (v);
  return 0;
}

Matrices¶

Matrices are defined by a gsl_matrix structure which describes a generalized slice of a block. Like a vector it represents a set of elements in an area of memory, but uses two indices instead of one.

type gsl_matrix¶

The gsl_matrix structure contains six components, the two dimensions of the matrix, a physical dimension, a pointer to the memory where the elements of the matrix are stored, data, a pointer to the block owned by the matrix block, if any, and an ownership flag, owner. The physical dimension determines the memory layout and can differ from the matrix dimension to allow the use of submatrices. The gsl_matrix structure is very simple and looks like this:

typedef struct
{
  size_t size1;
  size_t size2;
  size_t tda;
  double * data;
  gsl_block * block;
  int owner;
} gsl_matrix;

Matrices are stored in row-major order, meaning that each row of elements forms a contiguous block in memory. This is the standard “C-language ordering” of two-dimensional arrays. Note that Fortran stores arrays in column-major order. The number of rows is size1. The range of valid row indices runs from 0 to size1 - 1. Similarly size2 is the number of columns. The range of valid column indices runs from 0 to size2 - 1. The physical row dimension tda, or trailing dimension, specifies the size of a row of the matrix as laid out in memory.

For example, in the following matrix size1 is 3, size2 is 4, and tda is 8. The physical memory layout of the matrix begins in the top left hand-corner and proceeds from left to right along each row in turn.

01 02 03 XX XX XX XX
11 12 13 XX XX XX XX
21 22 23 XX XX XX XX

Each unused memory location is represented by “XX”. The pointer data gives the location of the first element of the matrix in memory. The pointer block stores the location of the memory block in which the elements of the matrix are located (if any). If the matrix owns this block then the owner field is set to one and the block will be deallocated when the matrix is freed. If the matrix is only a slice of a block owned by another object then the owner field is zero and any underlying block will not be freed.

The functions for allocating and accessing matrices are defined in gsl_matrix.h.

Matrix allocation¶

The functions for allocating memory to a matrix follow the style of malloc and free. They also perform their own error checking. If there is insufficient memory available to allocate a matrix then the functions call the GSL error handler (with an error number of GSL_ENOMEM) in addition to returning a null pointer. Thus if you use the library error handler to abort your program then it isn’t necessary to check every alloc.

gsl_matrix *gsl_matrix_alloc(size_t n1, size_t n2)¶: This function creates a matrix of size n1 rows by n2 columns, returning a pointer to a newly initialized matrix struct. A new block is allocated for the elements of the matrix, and stored in the block component of the matrix struct. The block is “owned” by the matrix, and will be deallocated when the matrix is deallocated. Requesting zero for n1 or n2 is valid and returns a non-null result.

gsl_matrix *gsl_matrix_calloc(size_t n1, size_t n2)¶: This function allocates memory for a matrix of size n1 rows by n2 columns and initializes all the elements of the matrix to zero.

void gsl_matrix_free(gsl_matrix *m)¶: This function frees a previously allocated matrix m. If the matrix was created using gsl_matrix_alloc() then the block underlying the matrix will also be deallocated. If the matrix has been created from another object then the memory is still owned by that object and will not be deallocated.

Accessing matrix elements¶

The functions for accessing the elements of a matrix use the same range checking system as vectors. You can turn off range checking by recompiling your program with the preprocessor definition GSL_RANGE_CHECK_OFF.

The elements of the matrix are stored in “C-order”, where the second index moves continuously through memory. More precisely, the element accessed by the function gsl_matrix_get(m,i,j) and gsl_matrix_set(m,i,j,x) is:

m->data[i * m->tda + j]

where tda is the physical row-length of the matrix.

double gsl_matrix_get(const gsl_matrix *m, const size_t i, const size_t j)¶: This function returns the $(i,j)$ -th element of a matrix m. If i or j lie outside the allowed range of 0 to n1 - 1 and 0 to n2 - 1 then the error handler is invoked and 0 is returned. An inline version of this function is used when HAVE_INLINE is defined.

void gsl_matrix_set(gsl_matrix *m, const size_t i, const size_t j, double x)¶: This function sets the value of the $(i,j)$ -th element of a matrix m to x. If i or j lies outside the allowed range of 0 to n1 - 1 and 0 to n2 - 1 then the error handler is invoked. An inline version of this function is used when HAVE_INLINE is defined.

double *gsl_matrix_ptr(gsl_matrix *m, size_t i, size_t j)¶
const double *gsl_matrix_const_ptr(const gsl_matrix *m, size_t i, size_t j)¶: These functions return a pointer to the $(i,j)$ -th element of a matrix m. If i or j lie outside the allowed range of 0 to n1 - 1 and 0 to n2 - 1 then the error handler is invoked and a null pointer is returned. Inline versions of these functions are used when HAVE_INLINE is defined.

Initializing matrix elements¶

void gsl_matrix_set_all(gsl_matrix *m, double x)¶: This function sets all the elements of the matrix m to the value x.

void gsl_matrix_set_zero(gsl_matrix *m)¶: This function sets all the elements of the matrix m to zero.

void gsl_matrix_set_identity(gsl_matrix *m)¶: This function sets the elements of the matrix m to the corresponding elements of the identity matrix, $m(i,j) = \delta(i,j)$ , i.e. a unit diagonal with all off-diagonal elements zero. This applies to both square and rectangular matrices.

Reading and writing matrices¶

The library provides functions for reading and writing matrices to a file as binary data or formatted text.

int gsl_matrix_fwrite(FILE *stream, const gsl_matrix *m)¶: This function writes the elements of the matrix m to the stream stream in binary format. The return value is 0 for success and GSL_EFAILED if there was a problem writing to the file. Since the data is written in the native binary format it may not be portable between different architectures.

int gsl_matrix_fread(FILE *stream, gsl_matrix *m)¶: This function reads into the matrix m from the open stream stream in binary format. The matrix m must be preallocated with the correct dimensions since the function uses the size of m to determine how many bytes to read. The return value is 0 for success and GSL_EFAILED if there was a problem reading from the file. The data is assumed to have been written in the native binary format on the same architecture.

int gsl_matrix_fprintf(FILE *stream, const gsl_matrix *m, const char *format)¶: This function writes the elements of the matrix m line-by-line to the stream stream using the format specifier format, which should be one of the %g, %e or %f formats for floating point numbers and %d for integers. The function returns 0 for success and GSL_EFAILED if there was a problem writing to the file.

int gsl_matrix_fscanf(FILE *stream, gsl_matrix *m)¶: This function reads formatted data from the stream stream into the matrix m. The matrix m must be preallocated with the correct dimensions since the function uses the size of m to determine how many numbers to read. The function returns 0 for success and GSL_EFAILED if there was a problem reading from the file.

Matrix views¶

type gsl_matrix_view¶
type gsl_matrix_const_view¶: A matrix view is a temporary object, stored on the stack, which can be used to operate on a subset of matrix elements. Matrix views can be defined for both constant and non-constant matrices using separate types that preserve constness. A matrix view has the type gsl_matrix_view and a constant matrix view has the type gsl_matrix_const_view. In both cases the elements of the view can by accessed using the matrix component of the view object. A pointer gsl_matrix * or const gsl_matrix * can be obtained by taking the address of the matrix component with the & operator. In addition to matrix views it is also possible to create vector views of a matrix, such as row or column views.

gsl_matrix_view gsl_matrix_submatrix(gsl_matrix *m, size_t k1, size_t k2, size_t n1, size_t n2)¶

gsl_matrix_const_view gsl_matrix_const_submatrix(const gsl_matrix *m, size_t k1, size_t k2, size_t n1, size_t n2)¶

These functions return a matrix view of a submatrix of the matrix m. The upper-left element of the submatrix is the element (k1, k2) of the original matrix. The submatrix has n1 rows and n2 columns. The physical number of columns in memory given by tda is unchanged. Mathematically, the $(i,j)$ -th element of the new matrix is given by:

m'(i,j) = m->data[(k1*m->tda + k2) + i*m->tda + j]

where the index i runs from 0 to n1 - 1 and the index j runs from 0 to n2 - 1.

The data pointer of the returned matrix struct is set to null if the combined parameters (i, j, n1, n2, tda) overrun the ends of the original matrix.

The new matrix view is only a view of the block underlying the existing matrix, m. The block containing the elements of m is not owned by the new matrix view. When the view goes out of scope the original matrix m and its block will continue to exist. The original memory can only be deallocated by freeing the original matrix. Of course, the original matrix should not be deallocated while the view is still in use.

The function gsl_matrix_const_submatrix() is equivalent to gsl_matrix_submatrix() but can be used for matrices which are declared const.

gsl_matrix_view gsl_matrix_view_array(double *base, size_t n1, size_t n2)¶

gsl_matrix_const_view gsl_matrix_const_view_array(const double *base, size_t n1, size_t n2)¶

These functions return a matrix view of the array base. The matrix has n1 rows and n2 columns. The physical number of columns in memory is also given by n2. Mathematically, the $(i,j)$ -th element of the new matrix is given by:

m'(i,j) = base[i*n2 + j]

where the index i runs from 0 to n1 - 1 and the index j runs from 0 to n2 - 1.

The new matrix is only a view of the array base. When the view goes out of scope the original array base will continue to exist. The original memory can only be deallocated by freeing the original array. Of course, the original array should not be deallocated while the view is still in use.

The function gsl_matrix_const_view_array() is equivalent to gsl_matrix_view_array() but can be used for matrices which are declared const.

gsl_matrix_view gsl_matrix_view_array_with_tda(double *base, size_t n1, size_t n2, size_t tda)¶

gsl_matrix_const_view gsl_matrix_const_view_array_with_tda(const double *base, size_t n1, size_t n2, size_t tda)¶

These functions return a matrix view of the array base with a physical number of columns tda which may differ from the corresponding dimension of the matrix. The matrix has n1 rows and n2 columns, and the physical number of columns in memory is given by tda. Mathematically, the $(i,j)$ -th element of the new matrix is given by:

m'(i,j) = base[i*tda + j]

where the index i runs from 0 to n1 - 1 and the index j runs from 0 to n2 - 1.

The new matrix is only a view of the array base. When the view goes out of scope the original array base will continue to exist. The original memory can only be deallocated by freeing the original array. Of course, the original array should not be deallocated while the view is still in use.

The function gsl_matrix_const_view_array_with_tda() is equivalent to gsl_matrix_view_array_with_tda() but can be used for matrices which are declared const.

gsl_matrix_view gsl_matrix_view_vector(gsl_vector *v, size_t n1, size_t n2)¶

gsl_matrix_const_view gsl_matrix_const_view_vector(const gsl_vector *v, size_t n1, size_t n2)¶

These functions return a matrix view of the vector v. The matrix has n1 rows and n2 columns. The vector must have unit stride. The physical number of columns in memory is also given by n2. Mathematically, the $(i,j)$ -th element of the new matrix is given by:

m'(i,j) = v->data[i*n2 + j]

where the index i runs from 0 to n1 - 1 and the index j runs from 0 to n2 - 1.

The new matrix is only a view of the vector v. When the view goes out of scope the original vector v will continue to exist. The original memory can only be deallocated by freeing the original vector. Of course, the original vector should not be deallocated while the view is still in use.

The function gsl_matrix_const_view_vector() is equivalent to gsl_matrix_view_vector() but can be used for matrices which are declared const.

gsl_matrix_view gsl_matrix_view_vector_with_tda(gsl_vector *v, size_t n1, size_t n2, size_t tda)¶

gsl_matrix_const_view gsl_matrix_const_view_vector_with_tda(const gsl_vector *v, size_t n1, size_t n2, size_t tda)¶

These functions return a matrix view of the vector v with a physical number of columns tda which may differ from the corresponding matrix dimension. The vector must have unit stride. The matrix has n1 rows and n2 columns, and the physical number of columns in memory is given by tda. Mathematically, the $(i,j)$ -th element of the new matrix is given by:

m'(i,j) = v->data[i*tda + j]

where the index i runs from 0 to n1 - 1 and the index j runs from 0 to n2 - 1.

The new matrix is only a view of the vector v. When the view goes out of scope the original vector v will continue to exist. The original memory can only be deallocated by freeing the original vector. Of course, the original vector should not be deallocated while the view is still in use.

The function gsl_matrix_const_view_vector_with_tda() is equivalent to gsl_matrix_view_vector_with_tda() but can be used for matrices which are declared const.

Creating row and column views¶

In general there are two ways to access an object, by reference or by copying. The functions described in this section create vector views which allow access to a row or column of a matrix by reference. Modifying elements of the view is equivalent to modifying the matrix, since both the vector view and the matrix point to the same memory block.

gsl_vector_view gsl_matrix_row(gsl_matrix *m, size_t i)¶

gsl_vector_const_view gsl_matrix_const_row(const gsl_matrix *m, size_t i)¶

These functions return a vector view of the i-th row of the matrix m. The data pointer of the new vector is set to null if i is out of range.

The function gsl_matrix_const_row() is equivalent to gsl_matrix_row() but can be used for matrices which are declared const.

gsl_vector_view gsl_matrix_column(gsl_matrix *m, size_t j)¶

gsl_vector_const_view gsl_matrix_const_column(const gsl_matrix *m, size_t j)¶

These functions return a vector view of the j-th column of the matrix m. The data pointer of the new vector is set to null if j is out of range.

The function gsl_matrix_const_column() is equivalent to gsl_matrix_column() but can be used for matrices which are declared const.

gsl_vector_view gsl_matrix_subrow(gsl_matrix *m, size_t i, size_t offset, size_t n)¶

gsl_vector_const_view gsl_matrix_const_subrow(const gsl_matrix *m, size_t i, size_t offset, size_t n)¶

These functions return a vector view of the i-th row of the matrix m beginning at offset elements past the first column and containing n elements. The data pointer of the new vector is set to null if i, offset, or n are out of range.

The function gsl_matrix_const_subrow() is equivalent to gsl_matrix_subrow() but can be used for matrices which are declared const.

gsl_vector_view gsl_matrix_subcolumn(gsl_matrix *m, size_t j, size_t offset, size_t n)¶

gsl_vector_const_view gsl_matrix_const_subcolumn(const gsl_matrix *m, size_t j, size_t offset, size_t n)¶

These functions return a vector view of the j-th column of the matrix m beginning at offset elements past the first row and containing n elements. The data pointer of the new vector is set to null if j, offset, or n are out of range.

The function gsl_matrix_const_subcolumn() is equivalent to gsl_matrix_subcolumn() but can be used for matrices which are declared const.

gsl_vector_view gsl_matrix_diagonal(gsl_matrix *m)¶

gsl_vector_const_view gsl_matrix_const_diagonal(const gsl_matrix *m)¶

These functions return a vector view of the diagonal of the matrix m. The matrix m is not required to be square. For a rectangular matrix the length of the diagonal is the same as the smaller dimension of the matrix.

The function gsl_matrix_const_diagonal() is equivalent to gsl_matrix_diagonal() but can be used for matrices which are declared const.

gsl_vector_view gsl_matrix_subdiagonal(gsl_matrix *m, size_t k)¶

gsl_vector_const_view gsl_matrix_const_subdiagonal(const gsl_matrix *m, size_t k)¶

These functions return a vector view of the k-th subdiagonal of the matrix m. The matrix m is not required to be square. The diagonal of the matrix corresponds to $k = 0$ .

The function gsl_matrix_const_subdiagonal() is equivalent to gsl_matrix_subdiagonal() but can be used for matrices which are declared const.

gsl_vector_view gsl_matrix_superdiagonal(gsl_matrix *m, size_t k)¶

gsl_vector_const_view gsl_matrix_const_superdiagonal(const gsl_matrix *m, size_t k)¶

These functions return a vector view of the k-th superdiagonal of the matrix m. The matrix m is not required to be square. The diagonal of the matrix corresponds to $k = 0$ .

The function gsl_matrix_const_superdiagonal() is equivalent to gsl_matrix_superdiagonal() but can be used for matrices which are declared const.

Copying matrices¶

int gsl_matrix_memcpy(gsl_matrix *dest, const gsl_matrix *src)¶: This function copies the elements of the matrix src into the matrix dest. The two matrices must have the same size.

int gsl_matrix_swap(gsl_matrix *m1, gsl_matrix *m2)¶: This function exchanges the elements of the matrices m1 and m2 by copying. The two matrices must have the same size.

Copying rows and columns¶

The functions described in this section copy a row or column of a matrix into a vector. This allows the elements of the vector and the matrix to be modified independently. Note that if the matrix and the vector point to overlapping regions of memory then the result will be undefined. The same effect can be achieved with more generality using gsl_vector_memcpy() with vector views of rows and columns.

int gsl_matrix_get_row(gsl_vector *v, const gsl_matrix *m, size_t i)¶: This function copies the elements of the i-th row of the matrix m into the vector v. The length of the vector must be the same as the length of the row.

int gsl_matrix_get_col(gsl_vector *v, const gsl_matrix *m, size_t j)¶: This function copies the elements of the j-th column of the matrix m into the vector v. The length of the vector must be the same as the length of the column.

int gsl_matrix_set_row(gsl_matrix *m, size_t i, const gsl_vector *v)¶: This function copies the elements of the vector v into the i-th row of the matrix m. The length of the vector must be the same as the length of the row.

int gsl_matrix_set_col(gsl_matrix *m, size_t j, const gsl_vector *v)¶: This function copies the elements of the vector v into the j-th column of the matrix m. The length of the vector must be the same as the length of the column.

Exchanging rows and columns¶

The following functions can be used to exchange the rows and columns of a matrix.

int gsl_matrix_swap_rows(gsl_matrix *m, size_t i, size_t j)¶: This function exchanges the i-th and j-th rows of the matrix m in-place.

int gsl_matrix_swap_columns(gsl_matrix *m, size_t i, size_t j)¶: This function exchanges the i-th and j-th columns of the matrix m in-place.

int gsl_matrix_swap_rowcol(gsl_matrix *m, size_t i, size_t j)¶: This function exchanges the i-th row and j-th column of the matrix m in-place. The matrix must be square for this operation to be possible.

int gsl_matrix_transpose_memcpy(gsl_matrix *dest, const gsl_matrix *src)¶: This function makes the matrix dest the transpose of the matrix src by copying the elements of src into dest. This function works for all matrices provided that the dimensions of the matrix dest match the transposed dimensions of the matrix src.

int gsl_matrix_transpose(gsl_matrix *m)¶: This function replaces the matrix m by its transpose by copying the elements of the matrix in-place. The matrix must be square for this operation to be possible.

int gsl_matrix_complex_conjtrans_memcpy(gsl_matrix_complex *dest, const gsl_matrix_complex *src)¶: This function makes the matrix dest the conjugate transpose of the matrix src by copying the complex conjugate elements of src into dest. This function works for all complex matrices provided that the dimensions of the matrix dest match the transposed dimensions of the matrix src.

Matrix operations¶

The following operations are defined for real and complex matrices.

int gsl_matrix_add(gsl_matrix *a, const gsl_matrix *b)¶: This function adds the elements of matrix b to the elements of matrix a. The result $a(i,j) \leftarrow a(i,j) + b(i,j)$ is stored in a and b remains unchanged. The two matrices must have the same dimensions.

int gsl_matrix_sub(gsl_matrix *a, const gsl_matrix *b)¶: This function subtracts the elements of matrix b from the elements of matrix a. The result $a(i,j) \leftarrow a(i,j) - b(i,j)$ is stored in a and b remains unchanged. The two matrices must have the same dimensions.

int gsl_matrix_mul_elements(gsl_matrix *a, const gsl_matrix *b)¶: This function multiplies the elements of matrix a by the elements of matrix b. The result $a(i,j) \leftarrow a(i,j) * b(i,j)$ is stored in a and b remains unchanged. The two matrices must have the same dimensions.

int gsl_matrix_div_elements(gsl_matrix *a, const gsl_matrix *b)¶: This function divides the elements of matrix a by the elements of matrix b. The result $a(i,j) \leftarrow a(i,j) / b(i,j)$ is stored in a and b remains unchanged. The two matrices must have the same dimensions.

int gsl_matrix_scale(gsl_matrix *a, const double x)¶: This function multiplies the elements of matrix a by the constant factor x. The result $a(i,j) \leftarrow x a(i,j)$ is stored in a.

int gsl_matrix_scale_columns(gsl_matrix *A, const gsl_vector *x)¶

This function scales the columns of the $M$ -by- $N$ matrix A by the elements of the vector x, of length $N$ . The $j$ -th column of A is multiplied by $x_j$ . This is equivalent to forming

$A \rightarrow A X$

where $X = \textrm{diag}(x)$ .

int gsl_matrix_scale_rows(gsl_matrix *A, const gsl_vector *x)¶

This function scales the rows of the $M$ -by- $N$ matrix A by the elements of the vector x, of length $M$ . The $i$ -th row of A is multiplied by $x_i$ . This is equivalent to forming

$A \rightarrow X A$

where $X = \textrm{diag}(x)$ .

int gsl_matrix_add_constant(gsl_matrix *a, const double x)¶: This function adds the constant value x to the elements of the matrix a. The result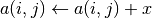 $a(i,j) \leftarrow a(i,j) + x$ is stored in a.

int gsl_matrix_complex_conjugate(gsl_matrix *a)¶: This function replaces each element of the matrix a with its complex conjugate value. The result $a(i,j) \leftarrow a(i,j)^{*}$ is stored in a.

Finding maximum and minimum elements of matrices¶

The following operations are only defined for real matrices.

double gsl_matrix_max(const gsl_matrix *m)¶: This function returns the maximum value in the matrix m.

double gsl_matrix_min(const gsl_matrix *m)¶: This function returns the minimum value in the matrix m.

void gsl_matrix_minmax(const gsl_matrix *m, double *min_out, double *max_out)¶: This function returns the minimum and maximum values in the matrix m, storing them in min_out and max_out.

void gsl_matrix_max_index(const gsl_matrix *m, size_t *imax, size_t *jmax)¶: This function returns the indices of the maximum value in the matrix m, storing them in imax and jmax. When there are several equal maximum elements then the first element found is returned, searching in row-major order.

void gsl_matrix_min_index(const gsl_matrix *m, size_t *imin, size_t *jmin)¶: This function returns the indices of the minimum value in the matrix m, storing them in imin and jmin. When there are several equal minimum elements then the first element found is returned, searching in row-major order.

void gsl_matrix_minmax_index(const gsl_matrix *m, size_t *imin, size_t *jmin, size_t *imax, size_t *jmax)¶: This function returns the indices of the minimum and maximum values in the matrix m, storing them in (imin, jmin) and (imax, jmax). When there are several equal minimum or maximum elements then the first elements found are returned, searching in row-major order.

Matrix properties¶

The following functions are defined for real and complex matrices. For complex matrices both the real and imaginary parts must satisfy the conditions.

int gsl_matrix_isnull(const gsl_matrix *m)¶
int gsl_matrix_ispos(const gsl_matrix *m)¶
int gsl_matrix_isneg(const gsl_matrix *m)¶
int gsl_matrix_isnonneg(const gsl_matrix *m)¶: These functions return 1 if all the elements of the matrix m are zero, strictly positive, strictly negative, or non-negative respectively, and 0 otherwise. To test whether a matrix is positive-definite, use the Cholesky decomposition.

int gsl_matrix_equal(const gsl_matrix *a, const gsl_matrix *b)¶: This function returns 1 if the matrices a and b are equal (by comparison of element values) and 0 otherwise.

double gsl_matrix_norm1(const gsl_matrix *A)¶: This function returns the 1-norm of the $m$ -by- $n$ matrix A, defined as the maximum column sum,

$||A||_1 = \textrm{max}_{1 \le j \le n} \sum_{i=1}^m |A_{ij}|$

Example programs for matrices¶

The program below shows how to allocate, initialize and read from a matrix using the functions gsl_matrix_alloc(), gsl_matrix_set() and gsl_matrix_get().

#include <stdio.h>
#include <gsl/gsl_matrix.h>

int
main (void)
{
  int i, j;
  gsl_matrix * m = gsl_matrix_alloc (10, 3);

  for (i = 0; i < 10; i++)
    for (j = 0; j < 3; j++)
      gsl_matrix_set (m, i, j, 0.23 + 100*i + j);

  for (i = 0; i < 100; i++)  /* OUT OF RANGE ERROR */
    for (j = 0; j < 3; j++)
      printf ("m(%d,%d) = %g\n", i, j,
              gsl_matrix_get (m, i, j));

  gsl_matrix_free (m);

  return 0;
}

Here is the output from the program. The final loop attempts to read outside the range of the matrix m, and the error is trapped by the range-checking code in gsl_matrix_get().

$ ./a.out
m(0,0) = 0.23
m(0,1) = 1.23
m(0,2) = 2.23
m(1,0) = 100.23
m(1,1) = 101.23
m(1,2) = 102.23
...
m(9,2) = 902.23
gsl: matrix_source.c:13: ERROR: first index out of range
Default GSL error handler invoked.
Aborted (core dumped)

The next program shows how to write a matrix to a file.

#include <stdio.h>
#include <gsl/gsl_matrix.h>

int
main (void)
{
  int i, j, k = 0;
  gsl_matrix * m = gsl_matrix_alloc (100, 100);
  gsl_matrix * a = gsl_matrix_alloc (100, 100);

  for (i = 0; i < 100; i++)
    for (j = 0; j < 100; j++)
      gsl_matrix_set (m, i, j, 0.23 + i + j);

  {
     FILE * f = fopen ("test.dat", "wb");
     gsl_matrix_fwrite (f, m);
     fclose (f);
  }

  {
     FILE * f = fopen ("test.dat", "rb");
     gsl_matrix_fread (f, a);
     fclose (f);
  }

  for (i = 0; i < 100; i++)
    for (j = 0; j < 100; j++)
      {
        double mij = gsl_matrix_get (m, i, j);
        double aij = gsl_matrix_get (a, i, j);
        if (mij != aij) k++;
      }

  gsl_matrix_free (m);
  gsl_matrix_free (a);

  printf ("differences = %d (should be zero)\n", k);
  return (k > 0);
}

After running this program the file test.dat should contain the elements of m, written in binary format. The matrix which is read back in using the function gsl_matrix_fread() should be exactly equal to the original matrix.

The following program demonstrates the use of vector views. The program computes the column norms of a matrix.

#include <math.h>
#include <stdio.h>
#include <gsl/gsl_matrix.h>
#include <gsl/gsl_blas.h>

int
main (void)
{
  size_t i,j;

  gsl_matrix *m = gsl_matrix_alloc (10, 10);

  for (i = 0; i < 10; i++)
    for (j = 0; j < 10; j++)
      gsl_matrix_set (m, i, j, sin (i) + cos (j));

  for (j = 0; j < 10; j++)
    {
      gsl_vector_view column = gsl_matrix_column (m, j);
      double d;

      d = gsl_blas_dnrm2 (&column.vector);

      printf ("matrix column %zu, norm = %g\n", j, d);
    }

  gsl_matrix_free (m);

  return 0;
}

Here is the output of the program,

matrix column 0, norm = 4.31461
matrix column 1, norm = 3.1205
matrix column 2, norm = 2.19316
matrix column 3, norm = 3.26114
matrix column 4, norm = 2.53416
matrix column 5, norm = 2.57281
matrix column 6, norm = 4.20469
matrix column 7, norm = 3.65202
matrix column 8, norm = 2.08524
matrix column 9, norm = 3.07313

The results can be confirmed using GNU octave:

$ octave
GNU Octave, version 2.0.16.92
octave> m = sin(0:9)' * ones(1,10)
               + ones(10,1) * cos(0:9);
octave> sqrt(sum(m.^2))
ans =
  4.3146  3.1205  2.1932  3.2611  2.5342  2.5728
  4.2047  3.6520  2.0852  3.0731

References and Further Reading¶

The block, vector and matrix objects in GSL follow the valarray model of C++. A description of this model can be found in the following reference,

B. Stroustrup, The C++ Programming Language (3rd Ed), Section 22.4 Vector Arithmetic. Addison-Wesley 1997, ISBN 0-201-88954-4.

Footnotes

1: Range checking is available in the GNU C Compiler bounds-checking extension, but it is not part of the default installation of GCC. Memory accesses can also be checked with Valgrind or the gcc -fmudflap memory protection option.