Sparse Matrices¶
This chapter describes functions for the construction and manipulation of sparse matrices, matrices which are populated primarily with zeros and contain only a few non-zero elements. Sparse matrices often appear in the solution of partial differential equations. It is beneficial to use specialized data structures and algorithms for storing and working with sparse matrices, since dense matrix algorithms and structures can be prohibitively slow and use huge amounts of memory when applied to sparse matrices.
The header file gsl_spmatrix.h contains the prototypes for the
sparse matrix functions and related declarations.
Data types¶
All the functions are available for each of the standard data-types.
The versions for double have the prefix gsl_spmatrix,
Similarly the versions for single-precision float arrays have the prefix
gsl_spmatrix_float. The full list of available types is given
below,
Prefix |
Type |
|---|---|
gsl_spmatrix |
double |
gsl_spmatrix_float |
float |
gsl_spmatrix_long_double |
long double |
gsl_spmatrix_int |
int |
gsl_spmatrix_uint |
unsigned int |
gsl_spmatrix_long |
long |
gsl_spmatrix_ulong |
unsigned long |
gsl_spmatrix_short |
short |
gsl_spmatrix_ushort |
unsigned short |
gsl_spmatrix_char |
char |
gsl_spmatrix_uchar |
unsigned char |
gsl_spmatrix_complex |
complex double |
gsl_spmatrix_complex_float |
complex float |
gsl_spmatrix_complex_long_double |
complex long double |
Sparse Matrix Storage Formats¶
GSL currently supports three storage formats for sparse matrices:
the coordinate (COO) representation, compressed sparse column (CSC)
and compressed sparse row (CSR) formats. These are discussed in more
detail below. In order to illustrate the different storage formats,
the following sections will reference this  -by-
-by- sparse matrix, with
sparse matrix, with  and
and  :
:
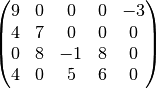
The number of non-zero elements in the matrix, also abbreviated as
nnz is equal to 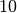 in this case.
in this case.
Coordinate Storage (COO)¶
The coordinate storage format, also known as triplet format,
stores triplets 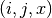 for each non-zero element of the matrix.
This notation means that the
for each non-zero element of the matrix.
This notation means that the  element of the matrix
element of the matrix  is
is  . The matrix is stored using three arrays of the same
length, representing the row indices, column indices, and matrix data. For
the reference matrix above, one possible storage format is:
. The matrix is stored using three arrays of the same
length, representing the row indices, column indices, and matrix data. For
the reference matrix above, one possible storage format is:
data |
9 |
7 |
4 |
8 |
-3 |
-1 |
8 |
5 |
6 |
4 |
row |
0 |
1 |
1 |
2 |
0 |
2 |
2 |
3 |
3 |
3 |
col |
0 |
1 |
0 |
1 |
4 |
2 |
3 |
2 |
3 |
0 |
Note that this representation is not unique - the coordinate triplets may
appear in any ordering and would still represent the same sparse matrix.
The length of the three arrays is equal to the number of non-zero elements
in the matrix, nnz, which in this case is 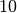 . The coordinate format is
extremely convenient for sparse matrix assembly,
the process of adding new elements, or changing existing elements, in a
sparse matrix. However, it is generally not suitable for the efficient
implementation of matrix-matrix products, or matrix factorization algorithms.
For these applications it is better to use one of the compressed formats
discussed below.
. The coordinate format is
extremely convenient for sparse matrix assembly,
the process of adding new elements, or changing existing elements, in a
sparse matrix. However, it is generally not suitable for the efficient
implementation of matrix-matrix products, or matrix factorization algorithms.
For these applications it is better to use one of the compressed formats
discussed below.
In order to faciliate efficient sparse matrix assembly, GSL stores
the coordinate data in a balanced binary search tree, specifically an AVL
tree, in addition to the three arrays
discussed above. This allows GSL to efficiently determine whether an
entry  already exists in the matrix, and to replace an existing
matrix entry with a new value, without needing to search unsorted arrays.
already exists in the matrix, and to replace an existing
matrix entry with a new value, without needing to search unsorted arrays.
Compressed Sparse Column (CSC)¶
Compressed sparse column storage stores each column of non-zero values in the sparse matrix in a continuous memory block, keeping pointers to the beginning of each column in that memory block, and storing the row indices of each non-zero element. For the reference matrix above, these arrays look like
data |
9 |
4 |
4 |
7 |
8 |
-1 |
5 |
8 |
6 |
-3 |
row |
0 |
1 |
3 |
1 |
2 |
2 |
3 |
2 |
3 |
0 |
col_ptr |
0 |
3 |
5 |
7 |
9 |
10 |
The data and row arrays are of length nnz and
are the same as the COO storage format. The col_ptr array
has length  , and
, and col_ptr[j] gives the index in
data of the start of column j. Therefore, the
 -th column of the matrix is stored in
-th column of the matrix is stored in
data[col_ptr[j]], data[col_ptr[j] + 1], …,
data[col_ptr[j+1] - 1].
The last element of col_ptr is nnz.
Compressed Sparse Row (CSR)¶
Compressed row storage stores each row of non-zero values in a continuous memory block, keeping pointers to the beginning of each row in the block and storing the column indices of each non-zero element. For the reference matrix above, these arrays look like
data |
9 |
-3 |
4 |
7 |
8 |
-1 |
8 |
4 |
5 |
6 |
col |
0 |
4 |
0 |
1 |
1 |
2 |
3 |
0 |
2 |
3 |
row_ptr |
0 |
2 |
4 |
7 |
10 |
The data and col arrays are of length nnz and
are the same as the COO storage format. The row_ptr array
has length  , and
, and row_ptr[i] gives the index in
data of the start of row i. Therefore, the
 -th row of the matrix is stored in
-th row of the matrix is stored in
data[row_ptr[i]], data[row_ptr[i] + 1],
…, data[row_ptr[i+1] - 1].
The last element of row_ptr is nnz.
Overview¶
These routines provide support for constructing and manipulating
sparse matrices in GSL, using an API similar to gsl_matrix.
The basic structure is called gsl_spmatrix.
-
type gsl_spmatrix¶
This structure is defined as:
typedef struct { size_t size1; size_t size2; int *i; double *data; int *p; size_t nzmax; size_t nz; [ ... variables for binary tree and memory management ... ] size_t sptype; } gsl_spmatrix;
This defines a
size1-by-size2sparse matrix. The number of non-zero elements currently in the matrix is given bynz. For the triplet representation,i,p, anddataare arrays of sizenzwhich contain the row indices, column indices, and element value, respectively. So if![data[k] = A(i,j)](_images/math/cacb5b457f3ad8aca39bc0d96cf4b6c363c7dd4c.png) , then
, then ![i = i[k]](_images/math/aace99a82c95b5669dfd6dc8b4af03d091434a2d.png) and
and ![j = p[k]](_images/math/3bbe6cef79f61a91cb47baf9156120d37afba17d.png) .
.For compressed column storage,
ianddataare arrays of sizenzcontaining the row indices and element values, identical to the triplet case.pis an array of sizesize2+ 1 wherep[j]points to the index indataof the start of columnj. Thus, if![data[k] = A(i,j)](_images/math/cacb5b457f3ad8aca39bc0d96cf4b6c363c7dd4c.png) , then
, then ![i = i[k]](_images/math/aace99a82c95b5669dfd6dc8b4af03d091434a2d.png) and
and ![p[j] <= k < p[j+1]](_images/math/87ba1005abed8a1b1d0758af2d2c7803cdbc60ba.png) .
.For compressed row storage,
ianddataare arrays of sizenzcontaining the column indices and element values, identical to the triplet case.pis an array of sizesize1+ 1 wherep[i]points to the index indataof the start of rowi. Thus, if![data[k] = A(i,j)](_images/math/cacb5b457f3ad8aca39bc0d96cf4b6c363c7dd4c.png) , then
, then ![j = i[k]](_images/math/16257b474203cde98d39998c85ad8f56f339601e.png) and
and ![p[i] <= k < p[i+1]](_images/math/5dde6383461957b3f4e6d62fe5395975b3a33b85.png) .
.There are additional variables in the
gsl_spmatrixstructure related to binary tree storage and memory management. The GSL implementation of sparse matrices uses balanced AVL trees to sort matrix elements in the triplet representation. This speeds up element searches and duplicate detection during the matrix assembly process. Thegsl_spmatrixstructure also contains additional workspace variables needed for various operations like converting from triplet to compressed storage.sptypeindicates the type of storage format being used (COO, CSC or CSR).The compressed storage format defined above makes it very simple to interface with sophisticated external linear solver libraries which accept compressed storage input. The user can simply pass the arrays
i,p, anddataas the inputs to external libraries.
Allocation¶
The functions for allocating memory for a sparse matrix follow the style of
malloc() and free(). They also perform their own error checking. If
there is insufficient memory available to allocate a matrix then the functions
call the GSL error handler with an error code of GSL_ENOMEM in addition
to returning a null pointer.
-
gsl_spmatrix *gsl_spmatrix_alloc(const size_t n1, const size_t n2)¶
This function allocates a sparse matrix of size
n1-by-n2and initializes it to all zeros. If the size of the matrix is not known at allocation time, bothn1andn2may be set to 1, and they will automatically grow as elements are added to the matrix. This function sets the matrix to the triplet representation, which is the easiest for adding and accessing matrix elements. This function tries to make a reasonable guess for the number of non-zero elements (nzmax) which will be added to the matrix by assuming a sparse density of . The function
. The function
gsl_spmatrix_alloc_nzmax()can be used if this number is known more accurately. The workspace is of size .
.
-
gsl_spmatrix *gsl_spmatrix_alloc_nzmax(const size_t n1, const size_t n2, const size_t nzmax, const size_t sptype)¶
This function allocates a sparse matrix of size
n1-by-n2and initializes it to all zeros. If the size of the matrix is not known at allocation time, bothn1andn2may be set to 1, and they will automatically grow as elements are added to the matrix. The parameternzmaxspecifies the maximum number of non-zero elements which will be added to the matrix. It does not need to be precisely known in advance, since storage space will automatically grow usinggsl_spmatrix_realloc()ifnzmaxis not large enough. Accurate knowledge of this parameter reduces the number of reallocation calls required. The parametersptypespecifies the storage format of the sparse matrix. Possible values are-
GSL_SPMATRIX_COO¶
This flag specifies coordinate (triplet) storage.
-
GSL_SPMATRIX_CSC¶
This flag specifies compressed sparse column storage.
-
GSL_SPMATRIX_CSR¶
This flag specifies compressed sparse row storage.
The allocated
gsl_spmatrixstructure is of size .
.-
GSL_SPMATRIX_COO¶
-
int gsl_spmatrix_realloc(const size_t nzmax, gsl_spmatrix *m)¶
This function reallocates the storage space for
mto accomodatenzmaxnon-zero elements. It is typically called internally bygsl_spmatrix_set()if the user wants to add more elements to the sparse matrix than the previously specifiednzmax.
Accessing Matrix Elements¶
-
double gsl_spmatrix_get(const gsl_spmatrix *m, const size_t i, const size_t j)¶
Initializing Matrix Elements¶
Since the sparse matrix format only stores the non-zero elements, it is automatically
initialized to zero upon allocation. The function gsl_spmatrix_set_zero() may
be used to re-initialize a matrix to zero after elements have been added to it.
-
int gsl_spmatrix_set_zero(gsl_spmatrix *m)¶
This function sets (or resets) all the elements of the matrix
mto zero. For CSC and CSR matrices, the cost of this operation is . For
COO matrices, the binary tree structure must be dismantled, so the cost is
. For
COO matrices, the binary tree structure must be dismantled, so the cost is
 .
.
Reading and Writing Matrices¶
-
int gsl_spmatrix_fwrite(FILE *stream, const gsl_spmatrix *m)¶
This function writes the elements of the matrix
mto the streamstreamin binary format. The return value is 0 for success andGSL_EFAILEDif there was a problem writing to the file. Since the data is written in the native binary format it may not be portable between different architectures.
-
int gsl_spmatrix_fread(FILE *stream, gsl_spmatrix *m)¶
This function reads into the matrix
mfrom the open streamstreamin binary format. The matrixmmust be preallocated with the correct storage format, dimensions and have a sufficiently largenzmaxin order to read in all matrix elements, otherwiseGSL_EBADLENis returned. The return value is 0 for success andGSL_EFAILEDif there was a problem reading from the file. The data is assumed to have been written in the native binary format on the same architecture.
-
int gsl_spmatrix_fprintf(FILE *stream, const gsl_spmatrix *m, const char *format)¶
This function writes the elements of the matrix
mline-by-line to the streamstreamusing the format specifierformat, which should be one of the%g,%eor%fformats for floating point numbers. The function returns 0 for success andGSL_EFAILEDif there was a problem writing to the file. The input matrixmmay be in any storage format, and the output file will be written in MatrixMarket format.
-
gsl_spmatrix *gsl_spmatrix_fscanf(FILE *stream)¶
This function reads sparse matrix data in the MatrixMarket format from the stream
streamand stores it in a newly allocated matrix which is returned in COO format. The function returns 0 for success andGSL_EFAILEDif there was a problem reading from the file. The user should free the returned matrix when it is no longer needed.
Copying Matrices¶
-
int gsl_spmatrix_memcpy(gsl_spmatrix *dest, const gsl_spmatrix *src)¶
This function copies the elements of the sparse matrix
srcintodest. The two matrices must have the same dimensions and be in the same storage format.
Exchanging Rows and Columns¶
-
int gsl_spmatrix_transpose_memcpy(gsl_spmatrix *dest, const gsl_spmatrix *src)¶
This function copies the transpose of the sparse matrix
srcintodest. The dimensions ofdestmust match the transpose of the matrixsrc. Also, both matrices must use the same sparse storage format.
-
int gsl_spmatrix_transpose(gsl_spmatrix *m)¶
This function replaces the matrix
mby its transpose, but changes the storage format for compressed matrix inputs. Since compressed column storage is the transpose of compressed row storage, this function simply converts a CSC matrix to CSR and vice versa. This is the most efficient way to transpose a compressed storage matrix, but the user should note that the storage format of their compressed matrix will change on output. For COO matrix inputs, the output matrix is also in COO storage.
Matrix Operations¶
-
int gsl_spmatrix_scale(gsl_spmatrix *m, const double x)¶
This function scales all elements of the matrix
mby the constant factorx. The result is stored in
is stored in m.
-
int gsl_spmatrix_scale_columns(gsl_spmatrix *A, const gsl_vector *x)¶
This function scales the columns of the
 -by-
-by- sparse matrix
sparse matrix
Aby the elements of the vectorx, of length . The
. The
 -th column of
-th column of Ais multiplied byx[j]. This is equivalent to forming
where
 .
.
-
int gsl_spmatrix_scale_rows(gsl_spmatrix *A, const gsl_vector *x)¶
This function scales the rows of the
 -by-
-by- sparse matrix
sparse matrix
Aby the elements of the vectorx, of length . The
. The
 -th row of
-th row of Ais multiplied byx[i]. This is equivalent to forming
where
 .
.
-
int gsl_spmatrix_add(gsl_spmatrix *c, const gsl_spmatrix *a, const gsl_spmatrix *b)¶
This function computes the sum
 . The three matrices must
have the same dimensions.
. The three matrices must
have the same dimensions.
-
int gsl_spmatrix_dense_add(gsl_matrix *a, const gsl_spmatrix *b)¶
This function adds the elements of the sparse matrix
bto the elements of the dense matrixa. The result is
stored in
is
stored in aandbremains unchanged. The two matrices must have the same dimensions.
-
int gsl_spmatrix_dense_sub(gsl_matrix *a, const gsl_spmatrix *b)¶
This function subtracts the elements of the sparse matrix
bfrom the elements of the dense matrixa. The result is
stored in
is
stored in aandbremains unchanged. The two matrices must have the same dimensions.
Matrix Properties¶
-
const char *gsl_spmatrix_type(const gsl_spmatrix *m)¶
This function returns a string describing the sparse storage format of the matrix
m. For example:printf ("matrix is '%s' format.\n", gsl_spmatrix_type (m));
would print something like:
matrix is 'CSR' format.
-
size_t gsl_spmatrix_nnz(const gsl_spmatrix *m)¶
This function returns the number of non-zero elements in
m.
-
int gsl_spmatrix_equal(const gsl_spmatrix *a, const gsl_spmatrix *b)¶
This function returns 1 if the matrices
aandbare equal (by comparison of element values) and 0 otherwise. The matricesaandbmust be in the same sparse storage format for comparison.
Finding Maximum and Minimum Elements¶
-
int gsl_spmatrix_minmax(const gsl_spmatrix *m, double *min_out, double *max_out)¶
This function returns the minimum and maximum elements of the matrix
m, storing them inmin_outandmax_out, and searching only the non-zero values.
-
int gsl_spmatrix_min_index(const gsl_spmatrix *m, size_t *imin, size_t *jmin)¶
This function returns the indices of the minimum value in the matrix
m, searching only the non-zero values, and storing them iniminandjmin. When there are several equal minimum elements then the first element found is returned.
Compressed Format¶
These routines calculate a compressed matrix from a coordinate representation.
-
int gsl_spmatrix_csc(gsl_spmatrix *dest, const gsl_spmatrix *src)¶
This function creates a sparse matrix in compressed sparse column format from the input sparse matrix
srcwhich must be in COO format. The compressed matrix is stored indest.Input matrix formats supported: COO
-
int gsl_spmatrix_csr(gsl_spmatrix *dest, const gsl_spmatrix *src)¶
This function creates a sparse matrix in compressed sparse row format from the input sparse matrix
srcwhich must be in COO format. The compressed matrix is stored indest.Input matrix formats supported: COO
-
gsl_spmatrix *gsl_spmatrix_compress(const gsl_spmatrix *src, const int sptype)¶
This function allocates a new sparse matrix, and stores
srcinto it using the format specified bysptype. The inputsptypecan be one ofGSL_SPMATRIX_COO,GSL_SPMATRIX_CSC, orGSL_SPMATRIX_CSR. A pointer to the newly allocated matrix is returned, and must be freed by the caller when no longer needed.
Conversion Between Sparse and Dense Matrices¶
The gsl_spmatrix structure can be converted into the dense gsl_matrix
format and vice versa with the following routines.
-
int gsl_spmatrix_d2sp(gsl_spmatrix *S, const gsl_matrix *A)¶
This function converts the dense matrix
Ainto sparse COO format and stores the result inS.Input matrix formats supported: COO
-
int gsl_spmatrix_sp2d(gsl_matrix *A, const gsl_spmatrix *S)¶
This function converts the sparse matrix
Sinto a dense matrix and stores the result inA.
Examples¶
The following example program builds a 5-by-4 sparse matrix and prints it in coordinate, compressed column, and compressed row format. The matrix which is constructed is

The output of the program is:
printing all matrix elements:
A(0,0) = 0
A(0,1) = 0
A(0,2) = 3.1
A(0,3) = 4.6
A(1,0) = 1
.
.
.
A(4,0) = 4.1
A(4,1) = 0
A(4,2) = 0
A(4,3) = 0
matrix in triplet format (i,j,Aij):
(0, 2, 3.1)
(0, 3, 4.6)
(1, 0, 1.0)
(1, 2, 7.2)
(3, 0, 2.1)
(3, 1, 2.9)
(3, 3, 8.5)
(4, 0, 4.1)
matrix in compressed column format:
i = [ 1, 3, 4, 3, 0, 1, 0, 3, ]
p = [ 0, 3, 4, 6, 8, ]
d = [ 1, 2.1, 4.1, 2.9, 3.1, 7.2, 4.6, 8.5, ]
matrix in compressed row format:
i = [ 2, 3, 0, 2, 0, 1, 3, 0, ]
p = [ 0, 2, 4, 4, 7, 8, ]
d = [ 3.1, 4.6, 1, 7.2, 2.1, 2.9, 8.5, 4.1, ]
We see in the compressed column output, the data array stores
each column contiguously, the array  stores
the row index of the corresponding data element, and the
array
stores
the row index of the corresponding data element, and the
array  stores the index of the start of each column in the
data array. Similarly, for the compressed row output, the
data array stores each row contiguously, the array
stores the index of the start of each column in the
data array. Similarly, for the compressed row output, the
data array stores each row contiguously, the array  stores the column index of the corresponding data element, and
the
stores the column index of the corresponding data element, and
the  array stores the index of the start of each row
in the data array.
array stores the index of the start of each row
in the data array.
#include <stdio.h>
#include <stdlib.h>
#include <gsl/gsl_spmatrix.h>
int
main()
{
gsl_spmatrix *A = gsl_spmatrix_alloc(5, 4); /* triplet format */
gsl_spmatrix *B, *C;
size_t i, j;
/* build the sparse matrix */
gsl_spmatrix_set(A, 0, 2, 3.1);
gsl_spmatrix_set(A, 0, 3, 4.6);
gsl_spmatrix_set(A, 1, 0, 1.0);
gsl_spmatrix_set(A, 1, 2, 7.2);
gsl_spmatrix_set(A, 3, 0, 2.1);
gsl_spmatrix_set(A, 3, 1, 2.9);
gsl_spmatrix_set(A, 3, 3, 8.5);
gsl_spmatrix_set(A, 4, 0, 4.1);
printf("printing all matrix elements:\n");
for (i = 0; i < 5; ++i)
for (j = 0; j < 4; ++j)
printf("A(%zu,%zu) = %g\n", i, j,
gsl_spmatrix_get(A, i, j));
/* print out elements in triplet format */
printf("matrix in triplet format (i,j,Aij):\n");
gsl_spmatrix_fprintf(stdout, A, "%.1f");
/* convert to compressed column format */
B = gsl_spmatrix_ccs(A);
printf("matrix in compressed column format:\n");
printf("i = [ ");
for (i = 0; i < B->nz; ++i)
printf("%d, ", B->i[i]);
printf("]\n");
printf("p = [ ");
for (i = 0; i < B->size2 + 1; ++i)
printf("%d, ", B->p[i]);
printf("]\n");
printf("d = [ ");
for (i = 0; i < B->nz; ++i)
printf("%g, ", B->data[i]);
printf("]\n");
/* convert to compressed row format */
C = gsl_spmatrix_crs(A);
printf("matrix in compressed row format:\n");
printf("i = [ ");
for (i = 0; i < C->nz; ++i)
printf("%d, ", C->i[i]);
printf("]\n");
printf("p = [ ");
for (i = 0; i < C->size1 + 1; ++i)
printf("%d, ", C->p[i]);
printf("]\n");
printf("d = [ ");
for (i = 0; i < C->nz; ++i)
printf("%g, ", C->data[i]);
printf("]\n");
gsl_spmatrix_free(A);
gsl_spmatrix_free(B);
gsl_spmatrix_free(C);
return 0;
}
References and Further Reading¶
The algorithms used by these functions are described in the following sources,
Davis, T. A., Direct Methods for Sparse Linear Systems, SIAM, 2006.
CSparse software library, https://www.cise.ufl.edu/research/sparse/CSparse
 -by-
-by- matrix
matrix 