4.3 Triangles
Construire un triangle quelconque ne comporte pas de difficulté, il suffit d’indiquer les coordonnées des trois sommets du polygone.
| figure |
figure := DrGeoFigure nouveau.
figure polygone: {0@0 . 5@0 . 2@3}
Exemple 4.9: Triangle quelconque
4.3.1 Isocèle
Un triangle isocèle possède plusieurs propriétés offrant des approches différentes dans sa construction. Nous les explorons dans les sections suivantes.
Côtés isométriques
Résultat mathématique. Un triangle ABC isocèle en A a ses côtés AB et AC isométriques.
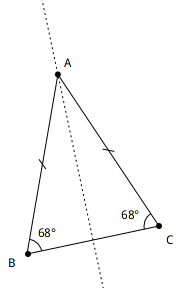
Figure 4.11: Triangle isocèle et côtés isométriques
Ainsi, étant donné un segment BC, le point A est construit au compas. Il est le point d’intersection de deux cercles de même rayon et de centre respectif B et C. Le rayon du cercle est la longueur des côtés AB et AC. Le triangle ABC est alors isocèle en A.
| figure b c cercle1 | figure := DrGeoFigure nouveau. b := (figure point: 5@1) nommer: 'B'. c := (figure point: 0@0) nommer: 'C'. cercle1 := figure cercleCentre: b rayon: 4
Exemple 4.10: Triangle isocèle et cercle
Compléter l’Exemple 4.10 pour construire le triangle ABC isocèle en A. Le point A sera construit comme l’intersection de deux cercles de rayon 4. Cacher les objets géométriques intermédiaires pour plus de clarté dans la figure finale.
Exercice 4.23: Triangle isocèle, côtés isométriques
Axe de symétrie
Résultat mathématique. Un triangle ABC isocèle en A admet comme axe de symétrie la médiatrice du segment BC.
Ou dit autrement, le point A appartient à la médiatrice du segment BC, cette médiatrice est également la hauteur issue de A du triangle ABC.
Connaissant B(5;1) et C(0;0), construire un point A sur la médiatrice du segment BC puis le triangle ABC. Utiliser les messages à mots-clés
médiatrice:etpointSurLigne:à:
Exercice 4.24: Triangle isocèle, axe de symétrie
Angles isométriques
Résultat mathématique. Un triangle ABC isocèle en A a ses angles B et C isométriques.
Ainsi, étant donnés un segment BC et une mesure d’angle choisie – par exemple 50 degrés – nous construisons au rapporteur deux demi-droites d’origine B et C et formant un angle de 50 degrés avec BC. Ces deux droites sont sécantes en A et le triangle ABC ainsi formé est isocèle en A.
Pour résumer, dans cette construction les étapes sont les suivantes :
- Choisir une mesure d’angle nommée alpha ;
- Construire les deux demi-droites d’origine B et C faisant un angle alpha avec la droite BC ;
- Construire A le point d’intersection de ces deux demi-droites.
Dr.Geo n’a pas d’outil de type rapporteur, la construction des demi-droites est donc délicate. Elle nécessite de s’appuyer sur la transformation géométrique rotation. Dans l’exemple suivant nous montrons le début du programme pour construire la demi-droite d’origine C format un angle donné avec BC.
| figure alpha1 b c b1 demiDroite1 | figure := DrGeoFigure nouveau. b := (figure point: 5@1) nommer: 'B'. c := (figure point: 0@0) nommer: 'C'. alpha1 := figure angleSommet: 10@10 de: 12@10 à: 12@13. b1 := figure rotationDe: b parCentre: c etAngle: alpha1. demiDroite1 := figure demiDroiteOrigine: c passantPar: b1
Exemple 4.11: Angle et rotation
Compléter l’Exemple 4.11 en construisant la demi-droite d’origine B et faisant un même angle avec BC, puis le point d’intersection A et le triangle ABC. Faire un croquis montrant la deuxième rotation nécessaire peut aider.
Exercice 4.25: Triangle isocèle et angle*
Dans la figure finale, ce qui serait amusant c’est de modifier l’angle à la souris. Pour cela il suffit de rendre visible un des points de l’angle, par exemple celui de coordonnées (12;10).
A la fin du programme de l’Exercice 4.25, rendre visible le point de coordonnées (12;10). Cacher tous les objets géométriques intermédiaires pour plus de clarté dans la figure finale.
Exercice 4.26: Triangle isocèle et angle variable
Dans les sections précédentes nous avons écrit trois programmes différents pour la construction d’un triangle isocèle. Selon la propriété du triangle isocèle utilisée, le programme était plus ou moins simple à concevoir. Souvent en informatique, il existe différentes approches pour résoudre un même problème. Une bonne connaissance du domaine – ici le triangle isocèle – permet de choisir la méthode la plus simple dans la conception du programme informatique. Ici s’appuyer sur l’axe de symétrie du triangle produisait clairement le programme le plus simple.
4.3.2 Équilatéral
Côtés isométriques
Résultat mathématique. Un triangle ABC équilatéral a ses côtés AB, AC et BC isométriques.
Ainsi étant donné un segment BC, le point A est construit au compas tel que BA=CA=BC. A est un point d’intersection des deux cercles de même rayon BC et de centre respectif B et C.
En complétant l’Exemple 4.10, écrire un programme pour construire le triangle ABC équilatéral. Le point A sera construit comme l’intersection de deux cercles de rayon BC. Cacher les objets géométriques intermédiaires pour plus de clarté dans la figure finale.
Exercice 4.27: Triangle équilatéral, côtés isométriques
Axes de symétrie
Résultat mathématique. Un triangle ABC équilatéral admet trois axes de symétrie, les médiatrices de ses trois côtés.
Ainsi étant donné un segment BC, le point A se construit comme une intersection de la médiatrice de BC et un cercle de centre B ou C et de rayon BC.
En complétant l’Exemple 4.10, écrire un programme pour construire le triangle ABC équilatéral. Le point A sera construit comme l’intersection de la médiatrice de BC et d’un cercle de rayon BC. Cacher les objets géométriques intermédiaires pour plus de clarté dans la figure finale.
Exercice 4.28: Triangle équilatéral, axes de symétrie
4.3.3 Triangle rectangle
Résultat mathématique. Un triangle ABC rectangle en B admet un angle droit ABC.
Connaissant B(5;1) et C(0;0), construire un point A sur la droite perpendiculaire au segment BC en B. Construire ensuite le triangle ABC. Utiliser les messages à mots-clés
perpendiculaireA:passantPar:etpointSurLigne:à:
Exercice 4.29: Triangle rectangle
4.3.4 Triangle rectangle isocèle
Résultat mathématique. Un triangle ABC isocèle rectangle en B admet un angle droit ABC et deux côtés isométriques BA et BC.
Connaissant B(5;1) et C(0;0), construire un point A sur la droite perpendiculaire au segment BC en B tel que BA=BC. Construire ensuite le triangle ABC. Utiliser les messages à mots-clés
perpendiculaireA:passantPar:etcercleCentre:passantPar:
Exercice 4.30: Triangle rectangle isocèle
Le codage permet de rendre visible des propriétés sur des angles ou des segments isométriques.
Reprendre la solution de l’Exercice 4.30 pour cacher les constructions intermédiaires, marquer les segments isométriques et afficher la valeur de l’angle droit. Utiliser les messages à mots-clés
angleGéométriqueSommet:de:à:etmarquerAvecSimpleTrait
Exercice 4.31: Triangle rectangle isocèle codé