4.2 Quadrilatères
4.2.1 Parallélogramme
Un parallélogramme possède plusieurs propriétés caractéristiques que nous utilisons pour le construire de différentes façons. Nous explorons celles-ci dans les sections suivantes.
Par les côtés opposés
Résultat mathématique. Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.
Étant donnés trois points A, B, C, le quatrième sommet D est construit comme l’intersection de la parallèle à AB passant par C et de la parallèle à BC passant par A.
| figure a b c d ab bc | figure := DrGeoFigure nouveau. a := (figure point: 1 @ 1) nommer: 'A'. b := (figure point: 5 @ 2) nommer: 'B'. c := (figure point: 6 @ 6) nommer: 'C'. ab := figure segmentDe: a à: b. bc := figure segmentDe: b à: c. d := figure intersectionDe: (figure parallèleA: ab passantPar: c) cacher et: (figure parallèleA: bc passantPar: a) cacher. d nommer: 'D'. figure segmentDe: a à: d. figure segmentDe: c à: d
Exemple 4.7: Parallélogramme et parallèles
Qu’observe-t-on lorsque les points A, B ou C sont déplacés ? Pourquoi ?
Exercice 4.7: Toujours parallélogramme
En suivant l’Exemple 4.7, construire le parallélogramme OMNP connaissant ses sommets M(-5;2) N(3;2) et P(1;-5). Il est conseillé de faire un croquis.
Exercice 4.8: Un autre parallélogramme
Résultat mathématique. Les cotés opposés d’un parallélogramme sont isométriques et parallèles.
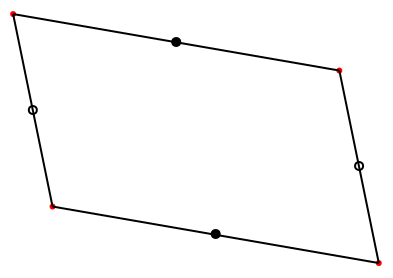
Figure 4.5: Côtés opposés du parallélogramme
C’est une propriété utilisée pour construire un parallélogramme au compas. Ici dans le code d’une figure programmée, nous utilisons des cercles dont les rayons sont les longueurs des côtés.
| figure o m n p mn pm cercle1 cercle2 | figure := DrGeoFigure nouveau. m := (figure point: -5 @ 2) nommer: 'M'. n := (figure point: 3 @ 2) nommer: 'N'. p := (figure point: 1 @ -5) nommer: 'P'. mn := figure segmentDe: m à: n. pm := figure segmentDe: p à: m. cercle1 := figure cercleCentre: p segment: mn. cercle1 tiret. cercle2 := figure cercleCentre: n segment: pm. cercle2 tiret. o := figure intersectionDe: cercle1 et: cercle2. o nommer: 'O'. figure segmentDe: o à: n. figure segmentDe: o à: p
Exemple 4.8: Parallélogramme et côtés isométriques
Une fois le code exécutée, dans la figure attraper et déplacer les points M, N ou P et observer la figure pour bien la comprendre.
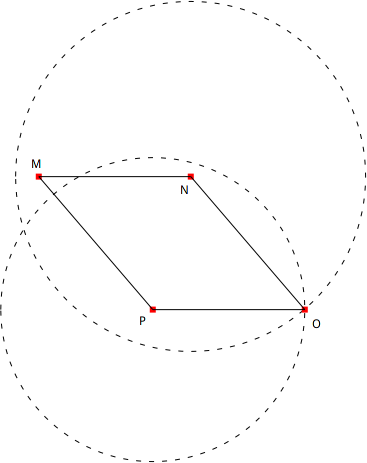
Figure 4.6: Parallélogramme et cercles
Les deux cercles de la Figure 4.6 se coupent en deux points dont l’un est le point O. Est-ce que le deuxième point d’intersection des deux cercles convient pour former un parallélogramme ? Pourquoi ?
Exercice 4.9: Deux points d’intersection
Par les diagonales
Résultat mathématique. Les diagonales d’un parallélogramme se coupent en leur milieu. Ce milieu est donc un centre de symétrie.
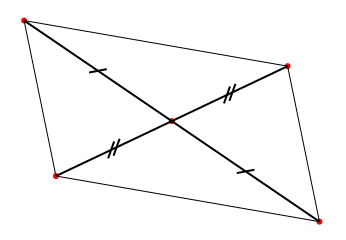
Figure 4.7: Diagonales du parallélogramme
Pour un parallélogramme ABCD dont I est le milieu de ses diagonales alors le point D est le symétrique de B par rapport à I. Cela nous fournit un programme de construction de ABCD que nous développons dans les deux exercices suivants.
Connaissant les points A(-5;2) B(3;2) et C(1;-5), construire le point I milieu de AC. Utiliser le message à mot clé
milieuDe:et:pour construire le milieu des points A et C.
Exercice 4.10: Parallélogramme et centre
L’Exercice 4.10 construit le point I, centre du
parallélogramme. Pour construire le parallélogramme ABCD, le point D
est construit comme symétrique de B par rapport à I avec le message
symétriqueDe:selonCentre:.
A partir de l’Exercice 4.10 construire le parallélogramme ABCD. Tracer ABCD avec un polygone.
Exercice 4.11: Parallélogramme et symétrie
4.2.2 Losange
Résultat mathématique. Un losange est un parallélogramme dont les côtés sont isométriques.
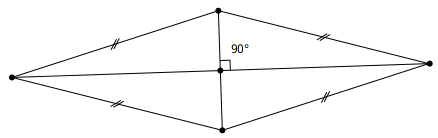
Figure 4.8: Losange
Troisième sommet
Ainsi pour un losange ABCD, connaissant A et B, le point C est tel que BA=BC. Pour placer correctement un point C, nous construisons le cercle de centre B et rayon BA, puis nous plaçons sur ce cercle un point C.
Programmer une figure avec les points A(0;0) et B(5;1), puis construire le cercle de centre B et passant par A. Sur ce cercle placer le point C d’abscisse 0.2. Utiliser les messages à mots clés
cercleCentre:passantPar:etpointSurLigne:à:
Exercice 4.12: Côtés adjacents isométriques
Par les côtés opposés
Une fois que les points A, B et C sont placés tel que BA=BC, il suffit de reprendre le programme de construction pour un parallélogramme : étant donnés trois points A, B, C, le quatrième sommet D est construit comme l’intersection de la parallèle à AB passant par C et de la parallèle à BC passant par A.
Compléter le code de l’Exercice 4.12 pour construire le point D afin que ABCD soit un parallélogramme. S’inspirer également du code de l’Exemple 4.7 pour cette construction.
Exercice 4.13: Losange comme un parallélogramme
Pour vérifier que le programme est valide, déplacer A, B et C afin d’observer ce qui se passe.
Par les diagonales
Résultat mathématique. Les diagonales d’un losange – en plus de se couper en leur milieu comme pour tout parallélogramme – sont perpendiculaires.
Lorsque les points A, B et C d’un losange ABCD sont placés sur la figure il est alors possible de construire le sommet D comme symétrique de B par rapport à I, milieu de AC.
Compléter le code de l’Exercice 4.12 pour construire le point D et le parallélogramme ABCD avec la méthode vue à l’Exercice 4.11.
Exercice 4.14: Losange et centre
4.2.3 Rectangle
Résultat mathématique. Un rectangle est un parallélogramme dont les côtés sont perpendiculaires.
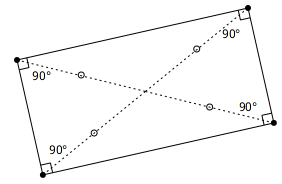
Figure 4.9: Rectangle
Troisième sommet
Ainsi pour un rectangle ABCD, connaissant les points A et B, le point C est tel que la droite BA est perpendiculaire à la droite BC. Pour placer correctement un point C, nous donc construisons la droite passant par B et perpendiculaire à la droite AB, puis nous plaçons sur cette droite un point C.
Programmer une figure avec les points A(0;0) et B(5;1), puis construire la droite passant par B et perpendiculaire à la droite AB. Sur cette droite placer le point C d’abscisse 0.1 Utiliser les messages à mots clés
perpendiculaireA:passantPar:etpointSurLigne:à:
Exercice 4.15: Côtés adjacents perpendiculaires
Par les côtés opposés
Une fois les trois points A, B et C placés comme dans l’Exercice 4.15, il suffit de reprendre le programme de construction pour un parallélogramme : étant donnés trois points A, B, C, le quatrième sommet D est construit comme l’intersection de la parallèle à AB passant par C et de la parallèle à BC passant par A.
Compléter le code de l’Exercice 4.15 pour construire le point D afin que ABCD soit un parallélogramme. S’inspirer également du code de l’Exemple 4.7 pour cette construction.
Exercice 4.16: Rectangle comme un parallélogramme
Par les diagonales
Résultat mathématique. Les diagonales d’un rectangle – en plus de se couper en leur milieu comme pour tout parallélogramme – sont isométriques.
Lorsque les points A, B et C d’un rectangle ABCD sont placés sur la figure il est alors possible de construire le sommet D comme symétrique de B par rapport à I, milieu de AC.
Compléter le code de l’Exercice 4.15 pour construire le point D et le parallélogramme ABCD avec la méthode vue à l’Exercice 4.11.
Exercice 4.17: Rectangle et centre
Autre approche. Puisque les diagonales du rectangle sont isométriques, nous commençons par la construction d’une diagonale, par exemple AC. La deuxième diagonale BD sera construite telle que BD=AC. Dans ce programme de construction nous utiliserons un cercle de diamètre AC.
Programmer une figure avec le segment d’extrémités les points A(0;0) et C(5;2). Construire le milieu I du segment AC puis le cercle de diamètre AC.
Exercice 4.18: Rectangle et cercle
Maintenant nous plaçons un point B où nous le souhaitons sur le cercle. La droite IB est construite puis le point D comme intersection entre la droite IB et le cercle.
Placer le point B d’abscisse 0.4 sur le cercle. Construire la droite IB et le point D comme d’intersection de IB et du cercle. Construire le polygone ABCD. Indices : utiliser les messages à mots clés
pointSurLigne:à:,droitePassantPar:et:etintersectionDe:et:
Exercice 4.19: Rectangle et diagonale
4.2.4 Carré
Résultat mathématique. Un carré est un parallélogramme dont les côtés sont isométriques et perpendiculaires. Le carré cumule les propriétés du losange et du rectangle, il est à la fois un losange et un rectangle.
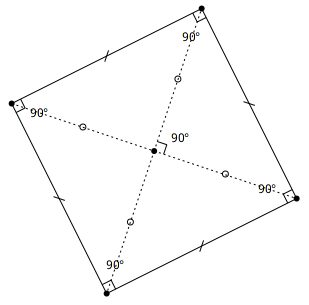
Figure 4.10: Carré
Troisième sommet
Ainsi pour un carré ABCD, connaissant A et B, le point C est tel que BA=BC et la droite BA est perpendiculaire à la droite BC.
Pour placer correctement un point C, nous construisons :
- la droite passant par B et perpendiculaire à la droite AB ;
- le cercle de centre B et passant par A ;
- le point C intersection de cette droite perpendiculaire avec ce cercle.
Programmer une figure avec les points A(0;0) et B(5;1). Construire la droite passant par B perpendiculaire à la droite AB puis le cercle de centre B passant par A. Enfin, construire le point C comme intersection de cette droite et de ce cercle. Indices : utiliser les messages à mots clés
perpendiculaireA:passantPar:,cercleCentre:passantPar:etintersectionDe:et:
Exercice 4.20: Côtés adjacents isométriques et perpendiculaires
Par les côtés opposés
Une fois les points A, B et C placés, il suffit de reprendre un programme de construction pour un parallélogramme déjà répété plusieurs fois.
Compléter le code de l’Exercice 4.20 pour construire le point D afin que ABCD soit un parallélogramme. S’inspirer également du code de l’Exemple 4.7 pour cette construction. Pour plus de clarté dans la figure finale, cacher les droites et cercle intermédiaires.
Exercice 4.21: Carré comme un parallélogramme
Par les diagonales
Résultat mathématique. Les diagonales d’un carré – en plus de se couper en leur milieu comme pour tout parallélogramme – sont isométriques et perpendiculaires.
Lorsque les points A, B et C d’un carré ABCD sont placés sur la figure il est alors possible de construire le sommet D comme symétrique de B par rapport à I, milieu de AC.
Compléter le code de l’Exercice 4.20 pour construire le point D et le carré ABCD avec la méthode vue à l’Exercice 4.11.
Exercice 4.22: Carré et centre