Droites (Programmer avec Dr.Geo)

Next: Quadrilatères, Up: Espace [Contents][Index]

4.1 Droites

4.1.1 Parallèles

Résultat mathématique. Deux droites d1 et d2 parallèles à une même troisième droite d3 sont parallèles entre elles. d1 // d3 et d2 // d3 ⇒ d1 // d2.

Cette proposition des éléments d’Euclide se traduit en un code simple :

| figure d1 d2 d3 |
figure := DrGeoFigure nouveau.
d1 := figure droitePassantPar: 0 @ 5 et: 2 @ 0.
d1 nommer: 'd1'.
(figure point: 0 @ 5) montrer.
d2 := figure parallèleA: d1 passantPar: 5 @ 0.
d2 nommer: 'd2'.
d3 := figure parallèleA: d1 passantPar: 6 @ 0.
d3 nommer: 'd3'

Exemple 4.1: Trois droites parallèles

Dans la figure, déplacer le point rouge et observer.

La 5ème ligne du code source force à rendre visible le point de coordonnées (0;5). Celui-ci est en effet ajouté à la figure en même temps que la droite d1, mais par défaut il est masqué à ce moment là pour ne pas surcharger la figure. Pour interagir avec la figure, il est intéressant de déplacer ce point là, nous le rendons donc visible.

Cette proposition est vraie pour 3 droites, écrire le programme pour construire les droites parallèles à d1 et passant par les points de l’axes des abscisses {3 ; 3.5 ; 4 ; 4.5 ;...; 12}

Exercice 4.1: Droites parallèles à la folie

4.1.2 Perpendiculaires

Résultat mathématique. Deux droites d1 et d2 perpendiculaires à une même troisième droite d3 sont parallèles entre elles.

Cette proposition des éléments d’Euclide se traduit également en un code simple :

| figure d1 d2 d3 |
figure := DrGeoFigure nouveau.
d1 := figure droitePassantPar: 0 @ 5 et: 2 @ 0.
d1 nommer: 'd1'.
(figure point: 0 @ 5) montrer.
d2 := figure perpendiculaireA: d1 passantPar: 0 @ 0.
d2 nommer: 'd2'.
d3 := figure perpendiculaireA: d1 passantPar: 6 @ 0.
d3 nommer: 'd3'

Exemple 4.2: Deux droites perpendiculaires

Dans la figure, déplacer le point rouge et observer.

Ecrire le programme pour construire les droites perpendiculaires à d1 et passant par les points de l’axes des abscisses {3 ; 3.5 ; 4 ; 4.5 ;...; 12}

Exercice 4.2: Droites perpendiculaires à la folie

Dans ce monde de grisaille – fond de figure blanc/noir et droite noire/blanche – ce serait revigorant de colorer les droites, par exemple :

| figure d1 droite |
figure := DrGeoFigure nouveau.
d1 := figure droitePassantPar: 0 @ 5 et: 2 @ 0.
d1 nommer: 'd1'.
(figure point: 0 @ 5) montrer.
3 à: 12 faire: [:abscisse |  
   droite := figure perpendiculaireA: d1 passantPar: abscisse @ 0.
   abscisse pair
      siVrai: [droite couleur: Color red]
      siFaux: [droite couleur: Color blue]
]

Exemple 4.3: Droites paires ou impaires colorées

La perpendiculaire créée est affectée à une variable droite. La boucle à:faire: parcourt les abscisses entières de 3 à 12. Dans cette boucle, la condition abscisse pair teste avec le message à mot clé siVrai:siFaux: si l’abscisse est paire ou impaire. Selon le cas, la droite est colorée en rouge ou en bleu.

Voici un exercice plus intéressant à faire :

Modifier l’Exemple 4.3 pour construire les perpendiculaires avec les abscisses entières de 1 à 500. Colorer en rouge les abscisses pairs, en orange les impairs et en bleu les nombres premiers. Modifier l’échelle de la figure à 3 pour une meilleure vue d’ensemble.

Exercice 4.3: Pair, impair, premier

Dans la figure produite, il est alors possible de reconnaître la séquence des nombres premiers parmi les nombres pairs et impairs.

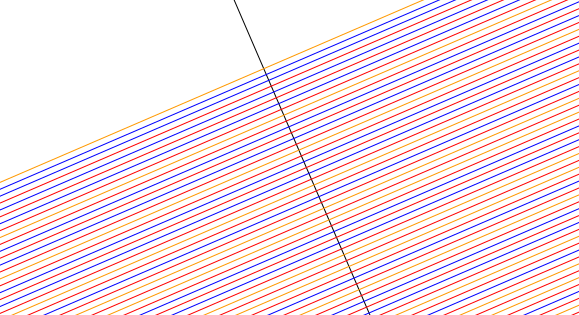
Figure 4.1: Les nombres premiers en bleu, parmi les autres nombres pairs et impairs non premiers, respectivement rouge et orange

4.1.3 Distance

4.1.3.1 Distance entre deux points

Résultat mathématique. La distance entre deux points est simplement la mesure du segment d’extrémités ces deux points.

| figure ptA ptB |
figure := DrGeoFigure nouveau afficherAxes.
ptA := figure point: 2 @ 3.
ptA nommer: 'A'.
ptB := (figure point: 3 @ -2) nommer: 'B'.
figure segmentDe: ptA à: ptB.
(figure distanceDe: ptA à: ptB) montrer

Exemple 4.4: Distance entre deux points

Dans la figure, en déplaçant à la souris les points A ou B, la distance est automatiquement actualisée. En attrapant la distance, des tirets rouges montrent qu’elle se rapporte aux points A et B.

4.1.3.2 Distance d’un point à une droite

Résultat mathématique. La distance entre un point et une droite est obtenue en construisant la droite perpendiculaire à la première droite et passant par le point. Ensuite mesurer la distance entre le point et l’intersection des deux droites. C’est le plus court chemin du point à la droite.

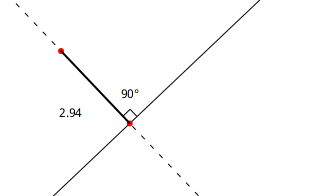
Figure 4.2: Distance d’un point à une droite

Pour réaliser la figure, nous introduisons un nouveau message à mot clé intersectionDe:et:. Ses paramètres sont les deux lignes dont nous souhaitons l’intersection.

| figure droite pointA perp intersection |
figure := DrGeoFigure nouveau.
droite := figure droitePassantPar: 5 @ 5 et: 7 @ -2.
pointA := figure point: -5 @ -5.
perp := figure perpendiculaireA: droite passantPar: pointA.
intersection := figure intersectionDe: droite et: perp.
(figure distanceDe: pointA à: intersection) montrer

Exemple 4.5: Distance d’un point à une droite

4.1.3.3 Distance entre deux droites parallèles

Résultat mathématique. La distance entre deux droites parallèles est obtenue en construisant une perpendiculaire à ces deux droites et en mesurant la distance entre leur intersection. C’est la longueur d’un plus court chemin entre ces deux droites.

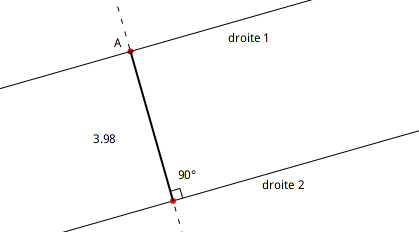
Figure 4.3: Distance entre deux droites parallèles

Dans l’exercice suivant, le programme pour produire une telle figure est partiellement écrit, il est à terminer.

Terminer l’écriture du programme ci-dessous pour construire la distance entre deux droites parallèles.
| figure droite1 droite2 perp pointA pointB | figure := DrGeoFigure nouveau afficherAxes. droite1 := figure droitePassantPar: 5 @ 5 et: 7 @ -2. droite2 := figure parallèleA: droite1 passantPar: 0 @ 0. perp := figure perpendiculaireA: droite2 passantPar: -5 @ 0. pointA := figure intersectionDe: droite1 et: perp. [...]

Exercice 4.4: Distance entre deux droites parallèles

Dans la figure produite à l’Exercice 4.4, que se passe-t-il lorsque la perpendiculaire est déplacée à la souris ?

Exercice 4.5: Déplacer la perpendiculaire

La distance entre deux droites parallèles s’obtient donc par la construction d’un chemin perpendiculaire entre celles-ci. Pour comparer avec d’autres chemins allant d’une droite à l’autre – et non perpendiculaires – il serait intéressant de construire un grand nombre de segments entre pointA et d’autres points sur droite2.

Mais avant cela, voici un exemple avec un autre chemin pour aller de droite1 à droite2. La longueur de ce chemin est plus grande que la distance !

| figure droite1 droite2 perp pointA autrePoint|
figure := DrGeoFigure nouveau afficherAxes.
droite1 := figure droitePassantPar: 5 @ 5 et: 7 @ -2.
droite2 := figure parallèleA: droite1 passantPar: 0 @ 0.
perp := figure perpendiculaireA: droite2 passantPar: -5 @ 0.
pointA := figure intersectionDe: droite1 et: perp.
autrePoint := figure pointSurLigne: droite2 à: 0.8.
(figure segmentDe: autrePoint à: pointA) pointillé

Exemple 4.6: Un autre chemin

Cet exemple introduit un nouveau message à mot clé pointSurLigne:à:. Il place un point sur une ligne. Son premier paramètre est une ligne – ici droite2 – et le deuxième paramètre est l’abscisse du point sur la ligne. Cette abscisse est une valeur décimale entre 0 et 1.

En adaptant l’Exemple 4.6, construire une série de segments d’extrémités pointA et des points sur droite2. Ces derniers sont construits à l’aide d’une boucle à:par:faire: de 0 à 1 par un pas de 0.01.

Exercice 4.6: D’autres chemins

Dans la figure déplacer la perpendiculaire et observer l’effet graphique !

Figure 4.4: Que de chemins !