2.7 Bloc de code

Jusqu’à présent, nous produisons des figures qui sont toujours identiques lors de l’exécution de son code source. Nous pouvons toutefois introduire du hasard en demandant de tirer au hasard un nombre entier qui servira d’abscisse ou d’ordonnée. Pour ce faire il suffit d’envoyer le message unaire auHasard à un nombre entier. Pour obtenir un nombre entier au hasard entre 1 et 5, écrire 5 auHasard.

DrGeoFigure nouveau
   afficherAxes
   point: 5 auHasard @ 5 auHasard

Là pour comprendre, il faut se souvenir de l’ordre d’envoi des messages. Le paramètre du message point: est 5 auHasard @ 5 auHasard. Les deux messages unaires auHasard sont envoyés avant le message @, ce qui donne un couple d’abscisse et d’ordonnée tirées au hasard pour les coordonnées du point.

Voici une variante de l’exemple précédent qui donne un résultat un peu différent :

DrGeoFigure nouveau
   afficherAxes;
   point: (11 auHasard - 6) @ (11 auHasard - 6)

Le point farceur

Ce qui serait amusant c’est de créer une figure avec un point farceur qui se déplace au hasard lorsque nous essayons de l’attraper. Pour ce faire, les coordonnées du point doivent être tirées au hasard à chaque instant. Il suffit que le code 5 auHasard @ 5 auHasard calculant les coordonnées soit exécuté à chaque instant, pour cela nous le transformons en un objet bloc de code.

Un bloc de code est un objet de type mini-programme qui s’exécute dans notre programme autant de fois que nous le souhaitons. Pour obtenir un bloc de code, il suffit de placer son code source entre crochets [ ]. Ainsi le paramètre du message à mot clé point: devient un bloc de code – bout de programme – qui sera exécuté à chaque fois que nous essayons d’attraper le point à la souris :

DrGeoFigure nouveau
   afficherAxes;
   point: [5 auHasard @ 5 auHasard]

Dans l’Exemple 2.21, le point farceur a des coordonnées qui sont toujours des nombres entiers. Nous aimerions avoir des valeurs décimales, par exemple au dixième près comme 2,4 ou 4,8. Pour y arriver, une astuce classique en informatique est de tirer au hasard un nombre entier plus grand de 1 à 50 – et non plus de 1 à 5 – et de diviser par 10. Le code devient alors 50 auHasard / 10.

DrGeoFigure nouveau
   afficherAxes;
   point: [(50 auHasard / 10) @ (50 auHasard / 10)]

Voici deux questions un peu difficiles sur le code de l’Exemple 2.22 :

Point farceur sur diagonale

Une chose encore plus forte est de forcer notre point farceur à rester sur la diagonale des axes des abscisses et des ordonnées. C’est-à-dire sur la droite qui passe par l’origine (0;0) du repère et le point (1;1).

Dans la Figure 2.4, si nous observons bien le point M situé sur cette diagonale, son abscisse et son ordonnée sont les mêmes.

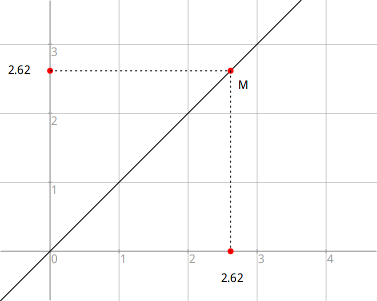
Figure 2.4: Point sur diagonale

Pour revenir à notre point farceur, pour le forcer à rester sur la diagonale il suffit que ses abscisse et ordonnée soient égales. Pour cela, nous utilisons une variable qui est locale au bloc de code et que nous déclarons au début du bloc avec le code | coordonnée |. Cette variable contient alors l’unique calcul d’une coordonnée tirée au hasard.

DrGeoFigure nouveau
   afficherAxes;
   afficherGrille;
   point: [
      | coordonnée |
      coordonnée := 50 auHasard / 10.
      coordonnée @ coordonnée
   ];
   droitePassantPar: 0@0 et: 1@1

A remarquer comment le bloc de code s’est étoffé sur plusieurs lignes. C’est en fait souvent le cas. La dernière ligne du bloc – coordonnée @ coordonnée – est la valeur retournée et qui sert à fixer les coordonnées du point farceur.

Pour plus de clarté, nous introduisons une variable figure pour lui envoyer des messages et éviter cette longue cascade de messages. Cela doit être la règle pour toute figure un temps soit peu complexe.

| figure |
figure := DrGeoFigure nouveau.
figure
   afficherAxes;
   afficherGrille.
figure point: [
   | coordonnée |
   coordonnée := 50 auHasard / 10.
   coordonnée @ coordonnée].
figure droitePassantPar: 0@0 et: 1@1