4.5 Angles
Depuis Dr.Geo, il est possible de construire deux types d’angle à partir de trois points :
- un angle géométrique dont la mesure est comprise entre
0° et 180°. Le message à envoyer à la figure
est
angleGéométriqueSommet:de:à:. - un angle orienté dont la mesure est comprise entre
0° et 360°. L’angle est orienté dans le sens
contraire des aiguilles d’une montre. Le message à envoyer à la
figure est
angleSommet:de:à:.
Observer comment les angles ci-dessous sont différents alors qu’ils sont construits à partir des mêmes points.
| figure | figure := DrGeoFigure nouveau. figure demiDroiteOrigine: 0@0 passantPar: -2@2. figure demiDroiteOrigine: 0@0 passantPar: 3@1. (figure angleGéométriqueSommet: 0@0 de: -2@2 à: 3@1) couleur: Color blue. (figure angleSommet: 0@0 de: -2@2 à: 3@1) couleur: Color brown
Exemple 4.12: Angles géométrique et orienté
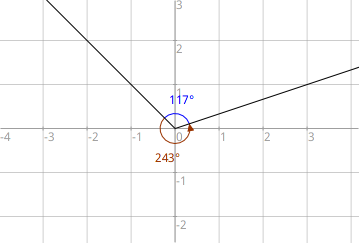
Figure 4.12: Angles géométrique (bleu) et orienté (marron avec flèche)
4.5.1 Angles correspondants
Résultat mathématique. Deux angles correspondants portés par deux droites parallèles sont isométriques.
Les angles sont placés du même côté des droites parallèles. Dans la figure ci-dessous, les droites AC et BD sont parallèles ; les angles BAC et EBD sont correspondants et isométriques.
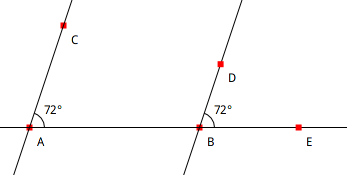
Figure 4.13: Angles correspondants portés par deux droites parallèles
Dans la figure interactive produite par le code ci-dessous, déplacer les points D et E de part et d’autre du point B pour observer le changement de mesure de l’angle EBD.
| figure a b c d e d1 d2 d3 | figure := DrGeoFigure nouveau. a:= (figure point: 0@0) nommer: 'A'. b:= (figure point: 5@0) nommer: 'B'. c:= (figure point: 1@3) nommer: 'C'. d1 := figure droitePassantPar: a et: b. d2 := figure droitePassantPar: a et: c. d3 := figure parallèleA: d2 passantPar: b. d:= (figure pointSurLigne: d3 à: 0.85) nommer: 'D'. e:= (figure pointSurLigne: d1 à: 0.96) nommer: 'E'. figure angleGéométriqueSommet: a de: b à: c. figure angleGéométriqueSommet: b de: e à: d
Exemple 4.13: Angles correspondants
4.5.2 Angles alternes-internes
Résultat mathématique. Deux angles alternes-internes portés par deux droites parallèles sont isométriques.
Les angles sont placés de part et d’autre de la troisième droite et entre les deux droites parallèles. Dans la figure ci-dessous, les droites AC et BD sont parallèles ; les angles BAC et EBD sont alternes-internes et isométriques.
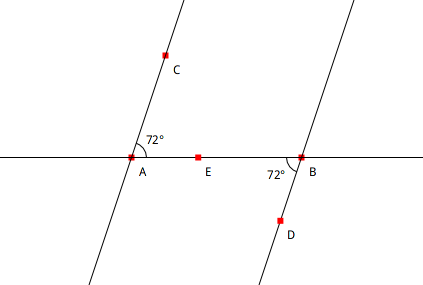
Figure 4.14: Angles alternes-internes portés par deux droites parallèles
Dans la figure interactive produite par le code ci-dessous, déplacer les points D et E de part et d’autre du point B pour observer le changement de mesure de l’angle EBD.
| figure a b c d e d1 d2 d3 | figure := DrGeoFigure nouveau. a:= (figure point: 0@0) nommer: 'A'. b:= (figure point: 5@0) nommer: 'B'. c:= (figure point: 1@3) nommer: 'C'. d1 := figure droitePassantPar: a et: b. d2 := figure droitePassantPar: a et: c. d3 := figure parallèleA: d2 passantPar: b. d:= (figure pointSurLigne: d3 à: 0.15) nommer: 'D'. e:= (figure pointSurLigne: d1 à: 0.85) nommer: 'E'. figure angleGéométriqueSommet: a de: b à: c. figure angleGéométriqueSommet: b de: e à: d
Exemple 4.14: Angles alternes-internes
4.5.3 Somme des angles d’un triangle
Résultat mathématique. La somme des angles d’un triangle est toujours égale à 180°.
Nous allons construire une figure expliquant cette propriété. Nous écrivons d’abord le code d’une figure d’un triangle avec ses sommets, ses côtés et ses angles.
| figure a b c ab bc | figure := DrGeoFigure nouveau. a := (figure point: 0@0) nommer: 'A'. b := (figure point: 6@0) nommer: 'B'. c := (figure point: 4@9) nommer: 'C'. (figure segmentDe: a à: b) normal. ab := figure droitePassantPar: a et: b. bc := (figure segmentDe: b à: c) normal. (figure segmentDe: a à: c) normal. (figure angleGéométriqueSommet: b de: a à: c) couleur: Color red. (figure angleGéométriqueSommet: a de: b à: c) couleur: Color blue. (figure angleGéométriqueSommet: c de: a à: b) couleur: Color brown
Exemple 4.15: Triangle et angles
Complétons maintenant ce code pour mettre en évidence deux angles particuliers de cette figure.
Compléter l’Exemple 4.15 en traçant une droite d1 passant par A et parallèle à BC. Placer sur d1 un point M d’abscisse 0.9 puis construire l’angle géométrique MAC. Que dire des angles ACB et MAC ?
Exercice 4.38: Triangle et angles
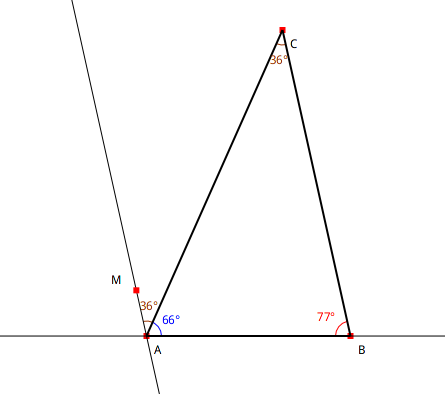
Figure 4.15: Triangle et angles alternes-internes
Nous complétons à nouveau le code de la figure pour mettre en évidence une autre paire d’angles particuliers.
Compléter le code de l’Exercice 4.38 en plaçant sur la droite AB un point N d’abscisse 0.2 puis construire l’angle géométrique MAN. Que dire des angles ABC et MAN ?
Exercice 4.39: Triangle et angles encore
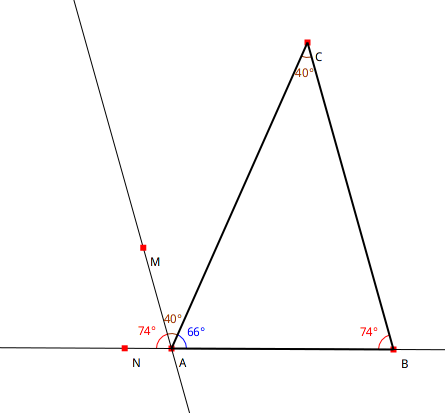
Figure 4.16: Triangle et angles correspondants
Que conclure sur la somme des angles d’un triangle ? Lorsque les points A, B ou C sont déplacés, la conclusion précédente est-elle toujours vraie ?
4.5.4 Somme des angles d’un quadrilatère
Résultat mathématique. Un polygone – quadrilatère – est convexe lorsqu’il contient chaque segment joignant deux de ses points.
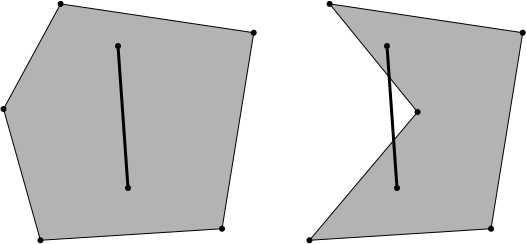
Figure 4.17: Polygones convexe et non convexe
En construisant une diagonale d’un quadrilatère convexe, cela revient à découper celui-ci en deux triangles. Il devient alors évident que la somme de ses angles est de 2 * 180°, soit 360°.
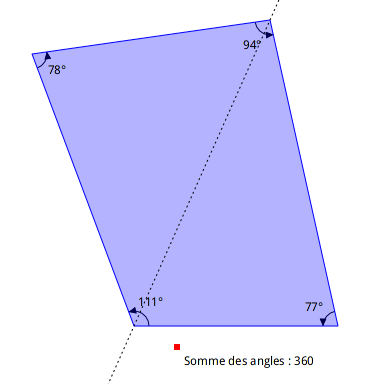
Figure 4.18: Somme des angles d’un quadrilatère convexe
Cette figure est produite avec le code suivant :
| figure ancre a b c d |
figure := DrGeoFigure nouveau.
figure polygone: { 0@0. 6@0. 4@9. -3@8 }.
(figure droitePassantPar: 0@0 et: 4@9) pointillé.
a := figure angleSommet: 0@0 de: 6@0 à: -3@8.
b := figure angleSommet: 6@0 de: 4@9 à: 0@0.
c := figure angleSommet: 4@9 de: -3@8 à: 6@0.
d := figure angleSommet: -3@8 de: 0@0 à: 4@9.
ancre := figure point: -2 @ -2.
figure point: [
ancre nommer: 'Somme des angles : ',
(a mathItem degreeAngle
+ b mathItem degreeAngle
+ c mathItem degreeAngle
+ d mathItem degreeAngle) arrondir asString]
Exemple 4.16: Angles d’un quadrilatère convexe
Observer comment la somme des angles est calculée : à chaque
angle a, b, c et d il est demandé son
modèle mathématique en lui envoyant le message mathItem. A
celui-ci, il est demandé la mesure de l’angle en degrés par le message
degreeAngle8.
Lorsque le quadrilatère est non-convexe et pour peu qu’il ne soit pas croisé – ses diagonales sont à l’intérieur du quadrilatère – le code de cette figure reste valide et la somme des angles est toujours de 360°.
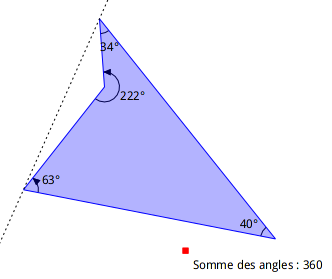
Figure 4.19: Somme des angles d’un quadrilatère non convexe, non croisé
En revanche, le code de cette figure ne convient pas pour afficher la somme des angles lorsque le quadrilatère est croisé. Certains angles se retrouvent à l’extérieur du quadrilatère. L’utilisation des angles orientés dans le code source ne convient pas dans ce cas.
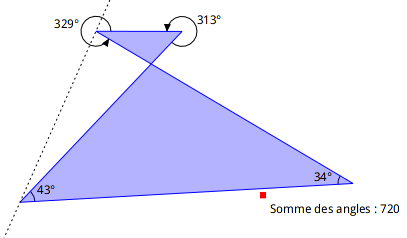
Figure 4.20: Somme des angles d’un quadrilatère non convexe, et croisé
Modifier le code de l’Exemple 4.16 pour afficher correctement les angles d’un quadrilatère croisé et ainsi avoir la somme correcte de ses angles. Indice : construire des angles géométriques avec le message
angleGéométriqueSommet:de:à:.
Exercice 4.40: Somme des angles d’un quadrilatère croisé
Dans la figure interactive alors produite, et en manipulant la diagonale, que conclure sur la somme des angles d’un quadrilatère croisé ?