This manual describes version 1.00.0 of GNU Backgammon.
Copyright © 1999, 2000, 2001, 2002, 2003 Achim Mueller, Gary Wong
Copyright © 2007 Christian Anthon
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.3 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled “GNU Free Documentation License”.Appendix A, GNU Free Documentation License.
Feedback
To report a bug or make a suggestion regarding the GNU Backgammon application or this
manual, send your suggestions to <bug-gnubg@gnu.org> or
make a bug
report.
| Revision History | |
|---|---|
| Revision GNU Backgammon Manual (docbook version) | February 2007 |
|
GNU Backgammon Project | |
| Revision GNU Backgammon Manual (wiki version) | January 2007 |
|
GNU Backgammon Project | |
| Revision GNU Backgammon Manual (texinfo version) | November 2003 |
|
GNU Backgammon Project | |
Abstract
The GNU Backgammon manual
Table of Contents
This manual describes how to use GNU Backgammon to play and analyse backgammon games and matches. It corresponds to version 1.00.0 (updated in August, 2013).
GNU Backgammon (gnubg) plays and analyses both money game sessions and tournament matches. It evaluates and rolls out positions, and much more. Driven by a command-line interface, it displays an ASCII rendering of a board on text-only terminals, but also allows the user to play games and manipulate positions with a graphical GTK+interface. GNU Backgammon is extensible on platforms which support Python.
 |
GNU Backgammon is a world class opponent and rates at around 2100 on FIBS, the First Internet Backgammon Server - at its best, it is in the top 5 of over 6000 rated players there). GNU Backgammon can be played on numerous other on-line backgammon servers.
The following features can be found in the current release of GNU Backgammon.
A command-line interface (with full command editing features if GNU readline is available) that lets you play matches and sessions against GNU Backgammon with a rough ASCII representation of the board on text terminals.
Support for a GTK+ graphical user interface with both 2D and 3D views of the board.
Tournament match and money session cube handling and cubeful play. All governed by an underlying cubeless money game based neural net.
Support for both 1-sided and 2-sided bearoff databases: 1-sided bearoff database for 15 checkers on the first 6 points and optional 2-sided database kept in memory. Larger 1-sided and 2-sided databases may be stored on disk.
Automated rollouts of positions, with lookahead and variance reduction where appropriate. Rollouts may be extended.
Automatic and manual annotation (analysis and commentary) of games and matches.
Record keeping of player statistics in games and matches using relational databases (SQLite, MySQL, and PostgreSQL are supported).
Loading and saving analysed games and matches as .sgf files (Smart Game Format).
Importing of positions, games and matches from a number of standard file formats, including: native GNU Backgammon file (.sgf), Jellyfish Match (.mat), GridGammon Save Game (.sgg), FIBS Oldmoves (.fibs), Jellyfish Position (.pos), Snowie Text (.txt), TrueMoneyGames (.tmg), GammonEmpire Game (.gam), PartyGammon Game (.gam), and BGRoom Game (.bgf).
Exporting of positions, games and matches to a number of standard file formats, including: native GNU Backgammon file (.sgf), Hypertext Markup Language (.html), Jellyfish Game (.gam), Jellyfish Match (.mat), Jellyfish Position (.pos), LaTeX (.tex), Portable Document Format (.pdf), Plain Text (.txt), Portable Network Graphics (.png), Postscript (.ps), Snowie Text (.txt), and Scalable Vector Graphics (.svg).
Python scripting ability.
Native language support; 15 languages are complete or in progress: (cs_CZ, da_DK, en_GB, en_US, es_ES, fi_FI, fr_FR, de_DE, el_GR, is_IS, it_IT, ja_JP, ro_RO, ru_RU and tr_TR)
GNU Backgammon is developed under the GNU General Public License (GPL) and it is part of the GNU project. For more information about the GNU project please visit their website: https://www.gnu.org/ For more information about free software in general please visit The Free Software Foundation at: https://www.fsf.org/.
This section describes how to play a game, a match, or a session of money games against GNU Backgammon or a human opponent. It is taken directly from the rules section of Backgammon Galore , courtesy of Tom Keith.
Backgammon is a game for two players, played on a board consisting of twenty-four narrow triangles called points. The triangles alternate in color and are grouped into four quadrants of six triangles each. The quadrants are referred to as a player's home board and outer board, and the opponent's home board and outer board. The home and the outer boards are separated from each other by a ridge down the center of the board called the bar.
An alternate arrangement is the reverse of the one shown here, with the home board on the left and the outer board on the right.
The points are numbered for either player starting in that player's home board. The outermost point is the twenty-four point, which is also the opponent's one point. Each player has fifteen checkers of his own color. The initial arrangement of checkers is: two on each player's twenty-four point, five on each player's thirteen point, three on each player's eight point, and five on each player's six point.
Both players have their own pair of dice and a dice cup used for shaking. A doubling cube, with the numerals 2, 4, 8, 16, 32, and 64 on its faces, is used to keep track of the current stake of the game.
The object of the game is for a player to move all of his checkers into his own home board and then bear them off. The first player to bear off all of his checkers wins the game.
To start the game, each player throws a single die. This determines both the player to go first and the numbers to be played. If equal numbers come up, then both players roll again until they roll different numbers. The player throwing the higher number now moves his checkers according to the numbers showing on both dice. After the first roll, the players throw two dice and alternate turns.
The roll of the dice indicates how many points, or pips, the player is to move his checkers. The checkers are always moved forward, to a lower-numbered point. The following rules apply:
A checker may be moved only to an open point, one that is not occupied by two or more opposing checkers.
The numbers on the two dice constitute separate moves. For example, if a player rolls 5 and 3, he may move one checker five spaces to an open point and another checker three spaces to an open point, or he may move the one checker a total of eight spaces to an open point, but only if the intermediate point (either three or five spaces from the starting point) is also open.
A player who rolls doubles plays the numbers shown on the dice twice. A roll of 6 and 6 means that the player has four sixes to use, and he may move any combination of checkers he feels appropriate to complete this requirement.
A player must use both numbers of a roll if this is legally possible (or all four numbers of a double). When only one number can be played, the player must play that number. Or if either number can be played but not both, the player must play the larger one. When neither number can be used, the player loses his turn. In the case of doubles, when all four numbers cannot be played, the player must play as many numbers as he can.
A point occupied by a single checker of either color is called a blot. If an opposing checker lands on a blot, the blot is hit and placed on the bar.
Any time a player has one or more checkers on the bar, his first obligation is to enter those checker(s) into the opposing home board. A checker is entered by moving it to an open point corresponding to one of the numbers on the rolled dice.
For example, if a player rolls 4 and 6, he may enter a checker onto either the opponent's four point or six point, so long as the prospective point is not occupied by two or more of the opponent's checkers.
If White rolls [64] with a checker on the bar, he must enter the checker onto Red's four point since Red's six point is not open. If neither of the points is open, the player loses his turn. If a player is able to enter some but not all of his checkers, he must enter as many as he can and then forfeit the remainder of his turn.
After the last of a player's checkers has been entered, any unused numbers on the dice must be played, by moving either the checker that was entered or a different checker.
Once a player has moved all of his fifteen checkers into his home board, he may commence bearing off. A player bears off a checker by rolling a number that corresponds to the point on which the checker resides, and then removing that checker from the board. Thus, rolling a 6 permits the player to remove a checker from the six point.
If there is no checker on the point indicated by the roll, the player must make a legal move using a checker on a higher-numbered point. If there are no checkers on higher-numbered points, the player is permitted (and required) to remove a checker from the highest point on which one of his checkers resides. A player is under no obligation to bear off if he can make an otherwise legal move.
A player must have all of his active checkers in his home board in order to bear off. If a checker is hit during the bear-off process, the player must bring that checker back to his home board before continuing to bear off. The first player to bear off all fifteen checkers wins the game.
Backgammon is played for an agreed stake per point. Each game starts at one point. During the course of the game, a player who feels he has a sufficient advantage may propose doubling the stakes. He may do this only at the start of his own turn and before he has rolled the dice.
A player who is offered a double may refuse, in which case he concedes the game and pays one point. Otherwise, he must accept the double and play on for the new higher stakes. A player who accepts a double becomes the owner of the cube and only he may make the next double.
Subsequent doubles in the same game are called redoubles. If a player refuses a redouble, he must pay the number of points that were at stake prior to the redouble. Otherwise, he becomes the new owner of the cube and the game continues at twice the previous stakes. There is no limit to the number of redoubles in a game.
At the end of the game, if the losing player has borne off at least one checker, he loses only the value showing on the doubling cube (one point, if there have been no doubles). However, if the loser has not borne off any of his checkers, he is gammoned and loses twice the value of the doubling cube. Or, worse, if the loser has not borne off any of his checkers and still has a checker on the bar or in the winner's home board, he is backgammoned and loses three times the value of the double cube.
The following optional rules are in widespread use.
Automatic doubles. If identical numbers are thrown on the first roll, the stakes are doubled. The doubling cube is turned to 2 and remains in the middle. Players usually agree to limit the number of automatic doubles to one per game.
Beavers. When a player is doubled, he may immediately redouble (beaver) while retaining possession of the cube. The original doubler has the option of accepting or refusing as with a normal double.
The Jacoby Rule. Gammons and backgammons count only as a single game if neither player has offered a double during the course of the game. This rule speeds up play by eliminating situations where a player avoids doubling so he can play on for a gammon.
When backgammon tournaments are held to determine an overall winner, the usual style of competition is match play. Competitors are paired off, and each pair plays a series of games to decide which player progresses to the next round of the tournament. This series of games is called a match.
Matches are played to a specified number of points. The first player to accumulate the required points wins the match. Points are awarded in the usual manner: one for a single game, two for a gammon, and three for a backgammon. The doubling cube is used, so the winner receives the value of the game multiplied by the final value of the doubling cube.
Matches are normally played using the Crawford rule. The Crawford rule states that if one player reaches a score one point short of the match, neither player may offer a double in the immediately following game. This one game with no doubling is called the Crawford game. If the Crawford game is won by the trailing player then the doubling cube becomes available in all subsequent games (and it's most often in the best interests of the trailing player to double immediately in these games).
| Match to 5 | White | Black | Doubling |
| White wins 2 | 2 | 0 | Allowed |
| Black wins 1 | 2 | 1 | Allowed |
| White wins 2 | 4 | 1 | Allowed |
| Black wins 1 | 4 | 2 | Crawford Game |
| Black wins 2 | 4 | 4 | Allowed |
| White wins 2 | 6 | 4 | Allowed |
In this example, White and Black are playing a 5-point match. After three games White has 4 points, which is just one point short of what he needs. That triggers the Crawford rule which says there can be no doubling in next game, Game 4.
There is no bonus for winning more than the required number of points in match play. The sole goal is to win the match, and the size of the victory doesn't matter.
Automatic doubles, beavers, and the Jacoby rule are not used in match play.
If GNU Backgammon is properly installed on your system, you can start it by simply typing gnubg at the command prompt. If you want to start the GNU Backgammon command-line interface, you can type gnubg --tty or gnubg -t. With this option, GNU Backgammon starts without the graphical user interface. There is also other options which can be added at the start-up.
The builds of GNU Backgammon which may be downloaded from the main GNU Backgammon page are packaged as an executable installer file. Running it will install GNU Backgammon and create a launch menu item in your start menu. Usually the menu item can be found by choosing → → → .
GNU Backgammon also has a command-line interface. This is supplied as a separate executable file on Microsoft Windows. You can start this version of GNU Backgammon by choosing → → → .
Once you have installed both an X11R6 server and GNU Backgammon for Mac OS X, you can run GNU Backgammon for Mac OS X by:
Start your X11R6 server;
Once your X11R6 server is running, in one of its Terminal windows (by default, Apple's X11 opens one such window at start-up, and XDarwin opens three), do the following:
If you have installed GNU Backgammon in your private Applications folder, type cd Applications/gnubg to get into GNU Backgammon for Mac OS X's folder, and then type ./gnubg to run it;
If you have installed GNU Backgammon in the global, top-level Applications folder, type cd /Applications/gnubg to get into GNU Backgammon for Mac OS X's folder, and type ./gnubg to run it;
The following options control the startup of GNU Backgammon. Most options are available in all versions of GNU Backgammon, but notably, the -w and -t options do not work under Microsoft Windows where separate command-line and GUI applications exist instead.
Example 1. GNU Backgammon startup options
Usage:
gnubg [OPTION?] [file.sgf]
Help Options:
-h, --help Show help options
--help-all Show all help options
--help-gtk Show GTK+ Options
Application Options:
-b, --no-bearoff Do not use bearoff database
-c, --commands=FILE Evaluate commands in FILE and exit
-l, --lang=LANG Set language to LANG
-p, --python=FILE Start in Python mode or evaluate code in FILE and exit
-q, --quiet Disable sound effects
-r, --no-rc Do not read .gnubgrc and .gnubgautorc commands
-S, --splash Show GTK splash screen
-t, --tty Start the command-line instead of using the graphical interface
-v, --version Show version information and exit
-w, --window-system-only Ignore tty input when using the graphical interface
-d, --debug Turn on debug
-D, --datadir Specify location of general data
-P, --pkgdatadir Specify location of program specific data
-O, --docdir Specify location of program documentation
-s, --prefsdir Specify location of user's preferences directory
--display=DISPLAY X display to use
To start a new game, match or session choose → , or use the button in the toolbar. This will open a dialog box, where you can select the main options for the new backgammon game you are about to begin.
The shortcut buttons are the quickest way to start the game or match. If you click on the button with the $ sign, you will start a new money game session immediately. If you click on a numbered button, you will start a new match of the specified length. If you click on the pencil-and-paper button you will start editing a position.
The dialog allows a fine tuning of the startup options:
In none of the above shortcuts is suitable, clicking OK will start a new match of the length set in the Match length field.
You may play against both the program itself or against a friend. If you want to start a match or game against a friend, select the Human vs. Human option.
Normally the dice are generated by a random number generator, but you may use manual dice if you check this option. Then GNU Backgammon will prompt for the dice roll before each roll.
GNU Backgammon comes with a tutor mode. If this mode is active, GNU Backgammon analyses each move you do, and warn you each time you make a mistake. More about tutor mode later.
By clicking on the Modify player settings... button, you will see the whole player setting dialog. Here you define the playing strength of GNU Backgammon. This dialog will be explained later.
The simplest way to roll the dice is to click in the right board area between the board points. You can also roll the dice from the menu → or with the keyboard shortcut Ctrl+R.
When you have moved your checkers to make the desired move, you complete your turn by clicking on the dice.
One way to move the checkers is to click on a checker you want to move and then drag it, while holding the mouse button down, to the desired designation point. If you have the option Show target help when dragging checkers enabled, you will see the a green guiding at any legal target point for the checker you are dragging. You can find this option by choosing → →
Move the mouse cursor over the checker you want to move. If you now click the left mouse button, the checker will move the pips of the left die. If you have already moved one checker, clicking on a new checker will move it according to the pips of the remaining die. If you click with the right mouse button on a checker, the checker will move according to the right die.
Using this method for moving the checkers can be really effective. Some users prefer showing the higher die to the left. You can make GNU Backgammon show the highest die to the left if you choose → → and check the check box labeled Show higher die on left.
Before you complete your move by clicking the dice, it's possible to undo your moves and return to the position before any checkers have been moved. You can either click the Undo button in the toolbar, or you can choose → from the menu or the keyboard shortcut Ctrl+Z.
There are some shortcuts for moving the checkers. You can make a new point by right clicking on the empty point that you want to make. As an example, if you roll 31 as the opening roll, and you want to play 8/5 6/5, you simply place the mouse cursor on the 5-point and right click. Making points this way also works if you hit a checker, and with doubles.
Another shortcut can be used in the bearoff phase of the game. By clicking in the bearoff tray, two checkers will be born off if such a move is legal.
GNU Backgammon can auto play forced moves for you. This feature can be enabled by choosing → → , and then check the box Play forced moves automatically.
You offer a double to your opponent by clicking on the cube. This will offer the cube immediately. You can also click → from the menu or the keyboard shortcut Ctrl+D.
You accept a double made by your opponent by clicking on the offered doubling cube at the board. If you want to decline the double, you can right click on the cube.
There are also three buttons in the toolbar for handling cube offers. These buttons are marked Accept, Decline and Beaver. The beaver button is only activated in money game sessions where beavers are allowed.
There are also menu options from the drop down menu for all the cube actions. Click → from the menu, to accept an offered double(Ctrl+T). Click → , from the menu, to to decline an offered double(Ctrl+P). Click → , from the menu, to beaver an offered double.
It's also possible to resign during a game. To resign during play press the Resign button in the toolbar. This is the button with the image of a white flag. When this button is pressed, a dialog box will appear where you can select if you want to resign a single game, gammon or backgammon. The resignation dialog may also be reached from the menu system. Click → to offer your resignation.
When a resignation is offered a white square will appear on the board area. The square has a number 1, 2 or 3. A square with a 1, means that a single game resignation is offered, a 2 that a gammon resignation is offered, and a 3, means that a backgammon is offered. If you're using a 3D board, the resignation will be a white flag instead of a square.
To accept the resignation click on the numbered square. If you want to decline the resignation, you right click instead. You can also use the same toolbar buttons as for accepting or declining a double. There is also a menu option for accepting and declining resignations. Click → from the menu, to accept an offered resignation. Click → from the menu, to decline an offered resignation.
If you want to get a hint of the best move or the best cube action press the Hint button in the tool bar or the menu option → . This will open a hint window.
This Hint window shows a list of all possible moves for the position and dice roll. The different moves are sorted by how GNU Backgammon ranks each move; there is one move on each line in the list. The rest of the numbers may look a bit complicated and cryptic but, once you learn what each number means, it isn't really that bad.
Rank is the number that shows GNU Backgammon's rank of the move. All moves evaluated at a given ply are ranked above those evaluated at a lesser ply. If you use the 0, 1, 2, etc, buttons below the hint list to re-evaluate one or more moves, the moves will be moved accordingly. Therefore, for accurate results when re-evaluating a move that you are interested in, it is usually best to re-evaluate all moves above it in the list. (And slipping with the mouse and re-evaluating, e.g., a 3-ply move at 2-ply may make the move disappear down to the bottom of the list!)
Type is a description of the evaluation that was used to calculate the results. Cubeful means that it is taking into account the possibility that someone may double. Occasionally you may see several moves with the equity of -1.000, (See Equity below), despite significantly different winning percentiles. This is because it thinks that if any of these moves are played then the opponent will double and you should pass. The n-ply is the depth to which GNU Backgammon analysed the move.
Win is the fractions of games that GNU Backgammon thinks will be won by a single game, gammon or backgammon.
Wg is the fractions of games that GNU Backgammon thinks will be won by a gammon or backgammon.
Wbg is the fractions of games that GNU Backgammon thinks will be won by a backgammon.
Lose is the fractions of games that GNU Backgammon thinks will be lost by a single game, gammon or backgammon. (Notice that this number is equal to 1 - Win)
Lg is the fractions of games that GNU Backgammon thinks will be lost by a gammon or backgammon.
Lbg is the fractions of games that GNU Backgammon thinks will be lost by a backgammon.
Equity is the overall evaluation of the position by the program, after considering the different win/loss percentiles, the cube position, and the match score. A 1.000 would mean that you are expected to win a point, a 0.000 would mean that it is roughly equal, and a -1.000 that you are expected to lose a point. When the evaluation is cubeful this number is not computable by the win/loss brake down of the previous columns.
Diff. is the difference in equity, perceived in comparison to the top ranked move.
Move is the move being evaluated. In the case of a red line, it is the move that was played.
If you're thinking about a cube decision before rolling you can press the same Hint button in the toolbar, as you pressed when you wanted checker play hint. The hint window will again appear, but this time it will look a bit different and it will show a hint of the correct cube decision.
The first lines is the window dialog shows the evaluation depth, and the cubeless equity with the evaluated probabilities. This equity is compensated for the match score. The cubeless equity for a money game, where the the calculation of equity is not compensated for match score, is also reported.
Next follow three lines with cubeful equities. In figure above, the cubeful equity for the player on roll for not doubling at this turn, is +0.123. The equity for a double and the opponent passing is (of course) +1.000, since the player then will win one point. (The number is normalized to cube value of one, so even if it is a redouble to 4 or 8 or higher, the cubeful equity for double/pass is still +1.000 for the doubler.) The third number in figure above is the cubeful equity for the player doubling and the opponent accepting the double. The different option will be listed in order with the best option highest. The number right to the listed equities is the differences from the cube decision considered best.
The last line states the best considered cube action. In the figure above, GNU Backgammon considers the best cube action to be No double, take. The number right to the proper cube action is the percentage of bad decisions by the taker that is needed to make a bad doubling decision against GNU Backgammon profitable against such an opponent. This number is only available when the position is considered No double, take or Too good to double, pass.
As you may see in both figures above, there is a set of buttons below the move list or cube analysis. Here follows a short description of what each of the buttons does:
Eval will evaluate the selected moves, or the cube decision with the current evaluation setting.
... will open the evaluation setting dialog. You can then modify the evaluation setting. More about evaluation settings in the next chapter.
0 1 2 3 4 will evaluate the selected moves or cube decision at cubeful 0-ply or cubeful 1-ply or cubeful 2-ply and so on.
Rollout will start a rollout ((A rollout is simply a Monte Carlo simulation of a backgammon position. More about rollouts in a later chapter.)) of the selected moves or cube decision.
... will open the rollout settings dialog. This dialog will be further described later in this manual.
MWC (Match Winning Chance). If this button is pressed the values in the hint window will be shown as the chance to win the whole match. If this button is unpressed or there is a money game that's played, the values in the hint window is reported as Equity. Notice, The equity in a match is actually a recalculation from match winning chance to equity. This recalculated number is often referred to as EMG, Equivalent to Money Game. The EMG number is comparable to the equity in a money game, and are therefore labeled 'Equity'.
Show will show the board as it would be after the selected move is made. The button is only available in the checker play hint window.
Move will make the move selected in the list. It's also possible to make a move directly from the list by double clicking on the move. The button is also available only in the checker play hint window.
Copy will copy the text of all selected moves to clipboard.
Temp. Map will show Sho Sengoku's temperature map. This map is further described later in the document. When this window remembers its size and position it will really become useful.
One of the greatest tools for learning, is Tutor Mode. Tutor mode can be activated by clicking → and then click on the Tutor flag. Activate Tutor Mode by checking the Tutor mode check box.
In Tutor Mode, GNU Backgammon will analyse your moves and/or cube decisions and compare them with its choices. You set the threshold for its alerts, for example, if you set it for bad then it will only warn you when you make a bad mistake. It will then allow you to re-examine your choice, go right ahead with it, or provide a 'hint' - essentially, showing you its analysis.
The tutor can give warnings on both cube decisions and checker play. If you want the tutor to only warn on cube decisions, you can uncheck the box for the Checker play. Likewise, if you want it to only warn on checker play decisions, you can uncheck the box for the Cube decisions.
In the above figure, you can see a warning dialog from the tutor mode. If you press the button labeled Play anyway, the move you made will be kept and the game will continue. If you press the Rethink button, the dialog will close and the checkers that you moved will be returned to their original positions. You can then rethink the position and try an alternative move. Keep doing this until the Tutor accepts your move as being good enough. Alternatively you can press the Hint button to show the hint window with its list of possible moves and their evaluations. Finally, if you press the End Tutor Mode button, the dialog will close and turn Tutor Mode off.
A similar warning window will also appear for poor cube handling.
Think about the Friday night chouette where there was this tough choice between two move candidates. Which move was the best? Or what about that match score cube decision from the weekend tournament. Wouldn't it be nice to be able to set up the position in GNU Backgammon and ask for its opinion? This is possible in GNU Backgammon, and it's one of the features that really can give you the answer to a lot of questions, and in that way give you a better understanding of the game.
To set up a position, you have to be in Edit mode. To enter Edit mode you simply click the Edit button in the tool bar and can start editing the current position. There is currently no keyboard shortcut or menu item for entering edit mode. The Edit button is a toggle button and you will stay in edit mode until you release the button by clicking it again.
If your Edit button in the toolbar is disabled it is because there is no game or match in progress hence no current position to edit. In this case you can use the button in the toolbar and then the pencil-and-paper button to enter Edit mode on the opening position of a unlimited session.
If used from a game in progress, this New-then-Edit sequence enters Edit mode on the current position after normalizing it with the player on roll on the bottom side and the match length set to unlimited session.
When you are in edit mode you will see the the text (Editing) in the match information box below the board.
Setting up a position is basically done by editing the current position. The editing it self is controlled by clicking different areas of the board and may not be obvious at first hand.
In edit mode you can easily clear the board by clicking in one of the bearoff trays. It's often easier to start setting up a position with a empty board, so this feature is really handy. When you click on one of the bearoff tray, all checkers will be moved to the bearoff.
You can also just as easy generate the initial position by clicking the opposite trays when in edit mode. Clicking in one of these trays puts all checkers back to the initial position.
Note that the bearoff trays change side when the board is displayed with clockwise movement.
In addition, both click-on-tray actions above reset the cube to centered with a value of 1 and clear the dice.
The default method of editing a position is called Quick edit. It's based on clicking on the point where you want to place checkers. The number of checkers placed on the point is depending on where you click, for example if you want to place 3 checkers on a point, clicking on the location where the third checker would go places 3 checkers. This method should be familiar to Snowie users.
Clicking with the left button places checkers for player1, clicking with the right button places checkers for player2. If you want to place more than 5 checkers, click multiple times on the tip of the point. To clear a point, click on the border of the board below or above the point - depending on if the point is in the lower or top half of the board. The bar works just like normal points - the more you click to the middle of the bar, the more checkers will be placed there.
There is also a different way of editing the checker positions. You can drag and drop checkers around the board while you're holding down the Ctrl key on your keyboard. Press the Ctrl key and hold it down. Then left-click the checker you want to drag to another point and drag it with the mouse, (while holding down the Ctrl key and the left mouse button), to the destination point. You can drag checkers to open points or to points where you have checkers of the same color. You can also 'hit' opponent blots with the drag and drop edit method.
This method of editing comes handy when there is just a small adjustment to be done in the position.
The player on turn can be set by clicking the small checker icons below the board. See figure below.
Figure 15. Clicking the White checker image will set White on turn, clicking the Black image will set Black in turn.
![[[initialboard.png]]](images/setturn.png)
Note that setting the turn sets the turn before the dice has been rolled. If there is a dice present at the board, setting the turn will remove the dice rolled. In this way you can set up a position to be a cube decision evaluation instead of a move decision evaluation.
The turn can also be set by choosing → . Both these methods for setting the player on turn can also be used without being in edit mode.
You can set the dice for a player by clicking in the middle part of the board where you usually click when you roll the dice while playing. Click in the middle of the right playing area to set the dice for player 0, the bottom player. Click the left dice rolling area to set the dice for player 1, the top player. Once you click one of these areas the dice selection widget will appear and you can select a dice roll by clicking on a dice pair.
Figure 16. Click inside the red rectangle to set the dice for Black. Click inside the green rectangle to set the dice for White.
![[[setdice.png]]](images/setdice.png)
Setting the dice in edit mode sets both dice and the player on turn. Setting the dice for player 0, will make player 0 on turn with that specific dice roll to play.
This method for setting the dice roll only works in edit mode. If you're not in edit mode you can set the dice by choosing → from the menu, however this will set the dice for the player on turn.
Setting the cube is quite simple while you're in edit mode. Simply click the cube in the board and the cube selection widget appears.
Selecting a cube in the first row, where the number is displayed up-side-down, the top player will be the cube owner. The value of the cube will be the value of the cube you click in the widget. Note that the unturned cube is the leftmost cube labeled 64, just as it usually is on real doubling cube.
Very often i backgammon the match score does matter on how the position is evaluated. GNU Backgammon's evaluation algorithms does take the score into account. You can therefore adjust the the match length and the score to each player while you're in edit mode.
In the figure you see that the score fields are editable while you're in edit mode. Insert the desired match score for each player in these fields. Player 0, the top player, has the left score field and player 1, the bottom player, has the right score. You can also set the match score in the in the match field to the right. There is also a box to tick whenever the position is from a Crawford game.
If you want the computer to do a money game evaluation of the position, you should set the match score to 0 (zero).
Before you can start analysing the position you have to exit edit mode. This is done by releasing the Edit button in the toolbar by clicking it. Note that editing a position destroys your game record with no warning, so it might be an idea to save your match if you want to keep it.
After you have successfully set up the position you desire, you can now analyse the position. You can click Hint in the toolbar to get the best move of cube decision in the same way as described in the chapter called the section called “Playing a game”. Hint, rollouts and evaluations done from the hint window will not be saved if you try to save the position. If you want to analyse the position and then be able to save the position and the analysis results you should rather do a move and then click back to the move and then choose → for the menu. You can then work in the analysis pane on the right side instead of in the hint window.
You can enter checkers on a point by clicking on the point. Notice the amount of checkers you add on a point, depends on where on that point you click. Left mouse button, black checkers and right mouse button, red checkers. (assuming you didn't change the colors). You will get used to this editing. and it makes it much faster to set up a position.
See also Albert Silver's post on GammOnLine
GNU Backgammon uses the Smart Game Format (SGF) to store games, matches, sessions and positions. SGF is used in as a standard format for several other turn based games. The SGF files can store all the rolls and moves and cube decisions as well as commentary and analysis.
A game that uses SGF extensively is Go. The format is described at this site.
Since version 0.16 the GUI recognizes all importable files automatically (with the exception of the FIBS format). To open or import a file choose → . A file dialog box will appear where you can select the file and the dialog will inform you of the recognized format, if the file is importable. You can also use the keyboard shortcut Ctrl-O, or the tool bar button labeled Open, to open the file dialog box directly.
It is still possible to import an unrecognized file by using the underlying command-line interface. Enable the command pane by choosing → . In the command pane type in import oldmoves <filepath> to import, e.g., an oldmoves fibs formatted file.
The following table contains the supported formats and the corresponding commands for manual import of a file.
| FIBS oldmoves format | import oldmoves <filepath> |
| GridGammon Save Game | import sgg <filepath> |
| GammonEmpire Game | import empire <filepath> |
| Jellyfish Game | import gam <filepath> |
| Jellyfish Match | import mat <filepath> |
| Jellyfish Position | import pos <filepath> |
| PartyGammon Game | import party <filepath> |
| Snowie Text | import snowietxt <filepath> |
| TrueMoneyGames | import tmg <filepath> |
Jellyfish Match is not formally defined and software exporting matches to this format often produce minor discrepancies. GNU Backgammon tries to cater to most of them automatically.
If you have played or imported a match into GNU Backgammon, and wish to save your efforts, you can choose → . A file dialog box will appear and you can type in a file name or keep the suggested default file name. (The suggested default file name contains the date, the players name and the length of the match). This will save the whole match of the current match or session. If there is any analysis or commentary available this will also be saved to the file. You can also use the tool bar button labeled Save to open the file dialog box directly. There is also a keyboard shortcut, Ctrl-S, for saving a match or session.
The export dialog is accessed by choosing → This dialog is similar to the save dialog. Again you may choose a different filename and whether to export an entire match, a game or a position. Then you must choose an export format as well. Notice some file formats only supports export of matches and some only supports position. Only when a legal combination is chosen will ending the dialog be possible. The following table contains the supported file formats and the corresponding commands for export. Again notice that with some formats only some of M(atch), G(ame), P(osition) is allowed. For example to export a Jellyfish position you would issue the command export position pos <filepath>
| HTML | export <MGP> html <filepath> |
| Jellyfish Game | export <G> gam <filepath> |
| Jellyfish Match | export <M> mat <filepath> |
| Jellyfish Position | export <P> pos <filepath> |
| LaTeX | export <MG> latex <filepath> |
| export <MG> pdf <filepath> | |
| Plain Text | export <MGP> text <filepath> |
| Portable Network Graphics | export <P> pdf <filepath> |
| PostScript | export <MGP> ps <filepath> |
| Scalable Vector Graphics | export <P> svg <filepath> |
| Snowie Text | export <MGP> snowietxt <filepath> |
GNU Backgammon can export the current position, game, match or session in HTML if you wish to publish it on the web.
GNU Backgammon exports in validating XHTML 1.0 with the use of CSS style sheets. You may add your own style sheet to the exported HTML files if you wish to override the default layout, e.g., change colors or fonts.
The board is made up from hundreds of pictures. Currently, you can choose between three different sets of pictures:
the BBS images used by Kit Woolsey's GammOnLine e-magazine, Stick's BGonline or the Danish Backgammon Federation's web-based discussion groups and others
the fibs2html images used by the Joseph Heled's program fibs2html
images generated by GNU Backgammon itself.
The images generated by GNU Backgammon will use your current board design in GNU Backgammon, and honors your settings on clockwise or anti-clockwise movement and board numbering (on, off, dynamic).
If you export a match or session to HTML, GNU Backgammon will write the individual games to separate files. For example, if you export to file foo.html the first game is exported to foo.html, the second game to foo_002.html, the third game to foo_003.html and so forth.
The output from the HTML export can be customized. For example, it's possible to leave out the analysis or parts of the analysis. Also, you may enter a specific URL to the pictures used to compose the board which is useful for posting positions on web-based discussion groups such as Stick's BGonline, Kit Woolsey's GammOnLine, or the Danish Backgammon Federation's Debat Forum.
If you want to have html images locally on your computer, you can have GNU Backgammon generate these. The html images will be generated based on the current appearance settings. You can also control the size of the images in the export settings dialog (To get the export settings dialog you can select in the menu → . Select the size of your html images at the bottom right in this dialog
To start the generation of the html images, select in the menu → → . In the file dialog box, you can select a directory where the images will be generated. The images are stored in PNG format.
To generate images from the command line, use the command:
export htmlimages directory
where directory is the directory where you want your images to be created.
GNU Backgammon can export games, match and positions to the document typesetting system LaTeX. For exporting a match or session to LaTeX
The LaTeX export will export all board diagrams and analysis if available. The produced documents can therefore be quite large. Note that the LaTeX file produced needs the eepic package. You can get this package at your nearest CTAN mirror (the produced LaTeX file also needs epic, textcomp and ucs, but these are more common in LaTeX distributions so you probably already have these).
Note that these prerequiste packages are only compatible with the original LaTeX, not PDFLaTeX.
It's possible to enter match transcriptions into GNU Backgammon. It's not very difficult. Presuming you're using the GUI, do this:
Start a match of any length, pressing the New button, and select Human-Human and manual dice.
To select the opening roll, click on the right dice pair in the dice selection window that appears. The left die in the dice pair is the die that's rolled by player 0, or the player at the top. The right die is the die that will be rolled by player 1 or the bottom player. So if you select for example the 53 dice combination it means that player 0 rolls a 5 and player 1 rolls a 3, and player 0 is therefore beginning this game. However, if you select the 35 dice combination it means that player 0 rolls a 3 and player 1 rolls a 5. Player 1 will therefore begin when you select 53 instead of 35.
To change the names, use the Edit button at the top. If you want to enter information such as the name of the Annotator, date, locale, etc. go to the Game menu and choose Match Information.
To enter written comments, you first have to play the move, and then go back to the move in the move list to be able to use the Commentary pane (feel free to close the Messages pane from the Windows menu). Don't forget to save the match every once in a while.
One comment: when entering the Cube commentary of a cube play (meaning it was turned), select the Take/Pass decision to enter the commentary. The reason is that if you export it after, and didn't do this, the commentary appears before the cube decision and not after as it should.
Tip: while entering the match, if you wish to see GNU Backgammon's opinion while you are entering the moves, play the move on the board and press the Hint button in the tool bar. In the latest builds, if you have done this, the results will then be placed with the move so that it means it is already analysed when you run the full match analysis. Mind you, it will preserve the information even if you ran a deeper 3-ply or 4-ply from the Hint window. After playing the move and confirming the dice, go back in the move list and click on the move, and you'll see the analysis appear in the Analysis pane as it should.
It's possible to enter illegal moves with a little trick. This is a step by step guide for the example: If a player rolls 41 and the player makes an illegal move as the dice showed 31.
Manually enter the roll which was rolled. 41.
Do a legal move with 41 (this is just to get the analysis of the roll, and the best legal move.)
Click the dice to pick them up and complete the move.
Now, before you roll the opponents dice, click the Edit button.
While holding down the CTRL-button on your keyboard, you can now drag the checkers to the resulting illegal position which was played over the board.
Release the Edit button to exit edit mode.
Make sure the right player is on turn, by clicking on the checker image for the player on roll, under the game board.
Continue to enter the rest of the game.
GNU Backgammon can analyse your matches for skill and luck. If you have an open match (as a result of playing, loading or importing), the analysis is started by choosing → . You should now see a progress bar at the bottom right corner of the main interface window while the computer is busy analysing. During this time you won't be able to interact with the program other than to quit the analysis. The analysis is complete when the progress bar disappears and you hear a small sound. Now, you would probably like to view the result of the analysis. This can be done in terms of overall statistics by choosing → , or in detail by browsing through the match. More on these subjects in the upcoming sections.
You can also analyse just the current game, by choosing → . If you're only interested in the analysis of the current move, you can select → .
You can configure how GNU Backgammon analysis the match or game for you. This can be configured in the dialog box that appears when choose → .
In the top left frame in this dialog box, you can select what to analyse. GNU Backgammon is able to analyse three different properties in a match.
Checker play
Cube decisions
Luck of each roll
In addition you can have the analysis to analyse just one of the players, or both. There is also possible to set a limit of how many moves to be analysed at each position. When you're reviewing your match, the number of analysed moves will be limited to number in this field. However, if you want to analyse further moves in a particular position, it's not a problem to do that later. The move that was actually done in the match will be analysed even if it is ranked below the number of moves limit.
GNU Backgammon will also mark each move or cube decision with Doubtful, Bad and Very bad. You can adjust the limits in equity difference for which label to assign. This is done in the frame box to the left. Notice, currently the Good and Very good classes are not used.
You can also adjust the classes for what GNU Backgammon considers lucky and unlucky rolls. The luck of a roll is defined as the difference of equity after the best move after rolled dice and the equity after best move averaged over all possible rolls.
The right part of the dialog box is an evaluation setting for how each move or cube decision should be evaluated in the analysis. For an explanation of this settings, see the chapter called "[[Evaluation settings]]".
When a match is analysed in GNU Backgammon you should open the game record window. Open this by checking → on from the main menu. The game record window can also be docked into the right side panel. If you want it docked into the right side panel you should check on → . The game record window shows a list of all the moves in the game. You can also navigate between the games and moves.
The figure shows a typical game record list. The moves are shown in two columns. The left column shows the moves for player 0,the to player, and the right column shows the moves of player 1, the bottom player. You can navigate through the game with the arrow buttons at the top of the game record. The red buttons with the double arrows take you to the previous game or the next match. (Arrow pointing to the left takes you to the previous game, and the red arrow pointing to the right takes you to the next game.) The green buttons take you one move ahead in the game or one move back. The green arrow button pointing to the right take you to the previous move. The green arrow button pointing to the right take you to the next move or to the next dice roll. If your in the move list where the dice is not rolled, a click on this green Next button will show you the same position with the dice rolled. The last two buttons take you to the next marked move, or to the previous marked move. The green arrow button with a question mark pointing to the left will take you to the previous marked move. The green arrow button with a question mark pointing to the right will take you to the next marked move. You can also go to other games in the match or session by selecting the game in the game drop down menu. You can also go to a move directly by clicking that move in the game record list.
There is also some keyboard shortcuts for navigating through the match. Page Down till take you to the next move and Page up will take you to the previous move.
After a analysis some of the move in the game list will be marked. You will see some moves marked with ? and some with ?! and some with ??. These marks means the same as the marks in normal chess notation.
| ?? | a very bad move |
| ? | a bad move |
| ?! | a doubtful move |
Note that it is the same marks for cube decisions as for checker moves. Nevertheless, checker moves marks are before the cube decisions marks. If no mark exists for checker move, the cube mark is separated by two spaces.
In newer builds of GNU Backgammon the various moves also get a color code. The cube decisions are shown by the background color. The checkers move decisions are shown by the font color.
| Cube(background) | Move(font) | |
| Very Bad | Yellow | Red |
| Bad | Pink | Blue |
| Doubtful | Grey | Green |
The luck is also marked in the font
| Luck | Font |
| Very Lucky | Bold |
| Very Unlucky | Italics |
You can also study your moves and cube decisions in more detail in the analysis window, or analysis panel if you have checked Dock panels in the Window menu. You can open this window by checking on → . If you have docked panels the analysis panel will appear under the game record. The analysis window is basically the same as the Hint window described in the "[[Playing a game or match]]" chapter.
In the figure you can see the analysis panel. At the top of the analysis panel you will see three pull-down menus. The leftmost pull-down menu is a comment on the cube decision. In the figure it is a position where the player didn't double and the GNU Backgammon's analysis of this is empty. There was nothing wrong with not doubling in this position. The user can also override GNU Backgammon's evaluation and mark the cube decision as 'Doubtful', 'Bad' or 'Very bad'. Note that the cube decision pull-down menu will only be visible when the player has the cube available.
The next pull-down menu shows a simple analysis of the roll. The roll in this position was 32. GNU Backgammon's evaluation of this dice roll is also empty. It shows that this particular roll was -.162 equity worse than the average roll. This means that the roll is a bit unlucky, but does not qualify for being marked as an unlucky roll. The rolls are marked in these categories: 'Very lucky', 'Lucky', 'Unlucky' and 'Very unlucky'.
The rightmost pull-down menu, shows the move which was done. In this situation the move that was done was 3/off 2/off. This move did not qualify for any mark. Moves that GNU Backgammon don't like will be marked as 'Doubtful', 'Bad' or 'Very bad'. The user can also override GNU Backgammon's evaluation and mark the move manually with the pull-down menu.
The rest of the analysis window is a notebook of two pages. The first page is the list of possible moves. The list is sorted in the ranked order with the best considered move at the top. The moves are sorted by equity or EMG. In the list in the figure there is only two possible moves. The move that was actually done in the match, is marked with red color. The only difference of this list of moves and the list of moves in the hint window, is that this list does not show the probabilities for each outcome of the game. If you want to see the probabilities of the different outcomes, you can click on the button labeled Details. This will then show you a list with these numbers.
The other page of the notebook is the cube decision analysis. This analysis show exactly the same as in the Hint window described in the chapter called "[[Playing a game or match]]". Note that the cube decision page will only be available if there is a cube decision. It will not be visible if the cube is not available to the player.
There is also a set of tool buttons in the analysis panel. These buttons does exactly the same as the tool buttons in the Hint window, which is described in the the chapter called "[[Playing a game or match]]".
You can get a summary of the analysis from the game, match, or session analysis. The game analysis is a summary for the current game whereas the match or session statistics is a summary of all the games in the match or session. The match analysis is available in the GUI from → or at the bottom of exported files.
This section provides a summary of the checker play statistics. The following information is available
Total moves: The total number of moves in the match.
Unforced moves: The number of unforced moves, i.e., all checker play decisions which had more than one legal move.
Moves marked xxx: The number of moves marked very good, very bad etc. The analysis will mark moves very bad, bad etc. based on the threshold you've defined in the analysis settings. GNU Backgammon can currently not automatically mark moves, e.g., good, but you can mark moves good yourself.
Error rate (total): The first number is the total amount of normalized equity that the player gave up during this game or match. The number in parenthesis is the un-normalized counterpart; for money play the all errors are multiplied with the value of the cube, and for match play the total match winning chance given up by the player is reported.
Error rate (per move): The error rate per move is the total error rate divided by the number of unforced moves. Note that is different from Snowie 4 that defines the error rate per move as the total error rate divided by the total number of moves for both players, i.e., the sum of total moves for both players. In general, your error rate per move will be lower in Snowie than in GNU Backgammon.
Checker play rating: GNU Backgammon will assign a rating for your checker play ranging from Awful! to Supernatural. See the description for the overall rating below.
This section provides information about how Ms. Fortuna distributed her luck. The following information is available:
Rolls marked xxx: The number of moves marked very lucky, lucky etc. Moves marked very lucky are huge jokers that improve your equity with more the +0.6 relative to the average equity. GNU Backgammon normally uses cubeful 0-ply evaluations to calculate the luck, but you can change that under the analysis settings. See below for a complete overview of what is considered very lucky, lucky, etc.
Luck rate (total): The total luck for this game or match reported both normalized and unnormalized.
Luck rate (per move): The luck rate per move reported both normalized and unnormalized.
Luck rating: Based on the luck rate per move GNU Backgammon will assign you a humorous luck rating. See below for the possible ratings.
Thresholds for marking of rolls:
| Deviation of equity from average | Roll is marked |
| > 0.6 | very lucky |
| 0.3 - 0.6 | lucky |
| -0.3 - 0.3 | unmarked |
| -0.6 - -0.3 | unlucky |
| < -0.6 | very unlucky |
Luck ratings:
| Normalized luck rate per move | Luck rating |
| > 0.06 | Go to Las Vegas |
| 0.03 - 0.06 | Good dice, man! |
| -0.03 - 0.03 | None |
| -0.06 - -0.03 | Bad dice, man! |
| < -0.06 | Go to bed |
This section provides a summary of the cube decision statistics: the number of cube decisions, missed doubles, etc.
Total cube decisions: The total number of cube decisions, i.e., the sum of no-doubles, doubles, takes, and passes.
Close or actual cube decisions: Similar to Total cube decisions, except that no-doubles are only included if they're considered close. GNU Backgammon considers a cube decision close if the relevant equities are within 0.16 from each other or if the position is too good.
Doubles, Takes, Passes: The total number of doubles, takes, and passes in the game or match.
Missed doubles around DP, Missed doubles around TG: The number of missed doubles around the double point and too good point respectively. If the equity is below 0.95 the position is considered to be around the double point else it considered to be around the too good point. If you miss doubles around the double point, it usually means that you double too late, whereas missed doubles around the too good point means that you're too greedy and play on for gammon when the position is not too good.
Wrong doubles around DP, Wrong doubles around TG: The number of wrong doubles around the double point and too good point, respectively. If you have wrong doubles around the double point that generally means that you double too early where you really should hold the cube, whereas wrong doubles around the too good point means that you double positions where you really should play on for a gammon or backgammon.
Wrong takes, Wrong passes: The total number of wrong takes and passes, respectively.
Error rate (total): The accumulated cube errors for this game or match reported both normalized and unnormalized.
Error rate (per cube decision): The error rate per cube decision is the total error rate divided by the number of close or actual cube decisions. Note that is different from Snowie 4 that defines the error rate per cube decision as the total error rate divided by the total number of moves for both players. In general, your error rate per cube decision will be lower in Snowie than in GNU Backgammon. Note that the reported number is multiplied by 1000 in the default settings.
Cube decision rating: GNU Backgammon will assign a rating for your cube decisions ranging from Awful! to Supernatural. See the description for the overall rating below.
The last section is the overall summary.
Error rate (total): The accumulated checker play and cube decision errors reported by normalized and unnormalized.
Error rate (per decision): The error rate per decision is the total error rate divided by the number of non-trivial decisions (i.e., the sum of unforced moves and close or actual cube decisions). Again, please note that is different from Snowie 4 that defines the error rate per decision as the total error rate divided by the total number of moves for both players. In general, your error rate per move will be lower in Snowie than in GNU Backgammon. An investigation of approximately 300 matches showed the on average the GNU Backgammon error rate with be 1.4 times higher than your Snowie 4 error rate.
Equivalent Snowie error rate: For easy comparison GNU Backgammon will also print the total error rate calculated by the same formula as Snowie 4.
Overall rating: Based on your normalized error rate per move GNU Backgammon will assign you a rating ranging from Awful! to Supernatural. See the table below for the thresholds.
Actual result: The actual result of the game or match. For money game this is simply the number of points won or lost during the game or match. For match play the number is calculated as 50% added to the result of the game or match in MWC. For example, losing a match or winning a match corresponds to an actual result of 0% and 100%, respectively. Winning 1 point in the first game of 7 point match is worth 6% using Kit Woolsey's match equity table, hence the actual result is 56%.
Luck adjusted result: The luck adjusted result is calculated as the actual result plus the total unnormalized luck rate. This is also called variance reduction of skill as described in Douglas Zare's excellent article Hedging Toward Skill. This should give an unbiased measure of the strengths of the players.
MWC against current opponent: For match play GNU Backgammon will calculate your MWC against the current opponent. The number is calculated as 50% - your total unnormalized error rate + your opponent's total unnormalized error rate. If your opponent is really lucky but plays rather bad, this number can become larger than 100%, since he due to the extra luck has the possibly to give up even more MWC. However, GNU Backgammon will report this number as 100%, and 0% for the opposite situation. Note that this number is biased towards the analysing bot, e.g., a 0-ply analysis a game between GNU Backgammon 2-ply and 0-ply will suggest that 0-ply is a favorite, which it is clearly not. For an unbiased measure use the luck adjusted result above.
Threshold for ratings:
| Normalized total error rate per move | Rating |
| 0.000 - 0.002 | Supernatural |
| 0.002 - 0.005 | World Class |
| 0.005 - 0.008 | Expert |
| 0.008 - 0.012 | Advanced |
| 0.012 - 0.018 | Intermediate |
| 0.018 - 0.026 | Casual Player |
| 0.026 - 0.035 | Beginner |
| > 0.035 | Awful! |
Please note: The Normalized total error rate per move is multiplied by 1000 in the default settings.
The million dollar question is simple enough: out of all the games that could result from playing this position, how many do we win (and how many of our wins and losses are gammons, and how many are backgammons)? The model is exactly the same as if we had an urn with a googol balls in it (it's a big urn), and many of the balls have win written on them, and some say gammon loss, and if we look hard enough there are a few that read backgammon win, and so on. (Balls and urns are to probability theorists what teapots and checkerboards are to computer graphics researchers, or squeamish ossifrage is to cryptographers; they seem to come with the territory.) Instead of having the patience to count the googol balls, we just give the urn a really good shake and then pull 100 balls out without looking, and say for instance "Well, I got 53 wins, 31 losses, 9 gammon wins, 6 gammon losses, and a backgammon win. It looks like my equity's roughly +0.26." and go home. If we were a bit more thorough, we could go a bit further and figure out that by cheating and measuring the sample proportions instead of the population proportions, we introduced a standard error of 0.06 into our result. (Of course, the trick is to select a sample size that's big enough that you reduce the standard error to a tolerable level, but small enough that the answer arrives before you get bored.)
It will come as no surprise that a rollout with a limited number of trials follows exactly the same procedure. It's sufficient to say that the proportion of wins/gammons etc. that come up when GNU Backgammon plays against itself (say) 1296 times, aren't likely to vary all that much from the proportion we would get if we measured the proportion of results in every game we could possibly get of GNU Backgammon playing against itself. (Of course, there may still be some doubt whether the results of GNU Backgammon vs. GNU Backgammon are representative of the results of a perfect player vs. a perfect player, or of you vs. Joe Average, but that's another story.)
In GNU Backgammon the Rollout function implements the procedure described above, with the following improvements:
Truncation: instead of rolling out all the way to the end of the game, it can stop and pretend its evaluation after a few plies is perfect. This may obviously introduce some amount of systematic error, but in practice this may not matter because:
it makes rollouts much faster, which means you can do more of them (and thus trade sampling error for systematic error);
different positions will be reached in different trials, so the correlation between errors in each trial weakens and the errors cancel out to some extent;
if you are rolling out the positions after making different plays, then any remaining systematic error between the two rollouts is likely to be somewhat correlated and so the error in the comparison between the plays is hopefully small. This implies that truncated rollouts are better for estimating relative equity (which is the better move here, 13/10*/9 or 13/10* 6/5*?) than absolute equity (at this match score I need 29% wins to accept a dead cube; can I take in this position?).
Race database truncation: when the game enters its 2-sided bearoff database, GNU Backgammon can estimate the probability of winning from that position with no error at all (it can play and evaluate endgame positions perfectly), which saves time and avoids introducing the errors that can result from large equity variances at the end of the game.
Variance reduction: when using lookahead evaluations, it can reduce errors by making use of the equity difference from one ply to the next. (This can be interpreted as either canceling out the estimated luck (i.e. the difference in equity evaluations before and after rolling) or using subsequent evaluations to estimate the error in prior ones; the two views are equivalent). GNU Backgammon automatically performs variance reduction when looking ahead at least one ply.
Stratified sampling: uses quasi-random number generation instead of pseudo-random number generation (this is a standard technique in Monte Carlo simulations where having a near-perfect uniform distribution in your sample is more important than unpredictability). GNU Backgammon only stratifies the first 2 plies of a rollout, though it would be easy enough to extend it to the remainder.
Quasi-Random Dice are used to reduce the element of luck in rollouts. Instead of selecting purely random dice, GNU Backgammon will ensure a uniform distribution of the first roll of the rollout. If 36 trials are requested, one game will start with 11, two games with 21, two games with 31, etc. In general, if n * 36 games is requested, n games will start with 11, 2*n games with 21 etc. This is called rotation of the first roll. Similarly, if n*1296 trials is requested, the second roll will be rotated, such that n games will start with 11-11, n games with 11-21, n games with 21-21, etc. The third roll be also be rotated if the number of trials is proportional to 46656.
Suppose a user stops a 1296 trial rollout after 36 games. The 36 games would have had the following rolls for the first two rolls of each game: 11-11, 21-11, 12-11, 31-11, 13-11, ..., 66-11 Obviously such a rollout will give skewed results since the second roll was 11 for all games! To avoid this problem GNU Backgammon will randomize the sequence of rolls such that it is guaranteed that for any sample of 36 games you have exactly one game with first roll 11, exactly one game with second roll 11, etc. This is called stratification.
GNU Backgammon will actually also rotate and stratify rollouts where the number of trials are not multiples of 36, 1296, etc. The distribution of rolls is obviously not uniform any longer in this case, but it will still provide some reduction of the luck, i.e., no 37 trial rollout will have 3 games with a initial 66.
Before the first game of a rollout, GNU Backgammon creates a pseudo random array which it will use for all the games in the rollout. In effect it has already decided the roll sequence it will use for up to 128 rolls in every game of the rollout. In other words, for a normal rollout where games don't go over 64 moves, every single game of every possible rollout length has already had its dice sequence determined. During the rollout of game n, sequence n will be used, for game n+1 sequence n+1, etc. If it's a rollout as initial position, then whenever the current sequence starts with a double, the sequence is skipped and the dice routine moves on to the next sequence. Say an rollout as initial position is about to start using sequence 275, but that sequence begins with a double. The dice routine moves to sequence 276. On the following game, it will use sequence 277 (it remembers how many it has already skipped).
So, if you select rollout as initial position and 36 games, then you will get a prefect set of rolls for games 1..30 and the first 6 rolls of the next perfect set (the same rolls you would have gotten for games 31..36 if you'd asked for 1080 games or 10800 games or 92 games or whatever.
The dice sequence doesn't know how many trials it will be asked for, it simply generates sequences such that for a normal rollout (rollout as initial position) every 36 (30) games you get all possible 1st rolls, every 1296 (1080) games get every possible first 2 rolls, every 46656 (38880) games you get full sets of 3 rolls, etc.
GNU Backgammon evaluation functionality is driven by 3 separate neural networks. The neural nets evaluates each position statically, and returns the outcome probabilities of the game at the given position. However, there are several different methods and techniques that an evaluation can use, and these can be adjusted. It's possible to set different levels of lookahead, it's possible to add noise to the evaluation, and each evaluation can be done cubeful or cubeless. All these setting together form a total evaluation setting. In GNU Backgammon there are several of these evaluations setting for each operation GNU Backgammon does.
Evaluation setting for Hints and Evaluations
Evaluation setting for analysis.
Evaluation setting for GNU Backgammon when it's playing.
Several evaluation settings for each move performed in a rollout.
A ply is simply considered to be one turn by a player. Any position can be evaluated at 0-ply. That means that GNU Backgammon does not look ahead in the game to evaluate the position. When GNU Backgammon is evaluating a checker play decision, it looks at all resulting positions after all the legal moves with the given dice roll, and evaluates these position at the given ply. It's possible to set the search depth by specifying the plies lookahead in any evaluation settings dialog.
Snowie and XG users: GNU Backgammon differs from most other software, notably Snowie and eXtreme Gammon in that GNU Backgammon starts counting plies at 0 (no lookahead) while other start at 1 ply. In the same way what is called 2-ply in GNU Backgammon will be similar to a Snowie 3-ply.
For GNU Backgammon, a 0-ply evaluation of a move would be done by:
Build a list of all legal moves. For each move, take the resulting board position and use the neural net to estimate the expected percentage of wins/gammons/backgammons/losses/gammon losses/backgammon losses. Rank the moves based on this evaluation.
For one ply, after doing the above step, GNU Backgammon chooses the best n moves (where n is set by the move filters). For each one, it takes the resulting position for that move and goes through all 21 possible dice rolls for the opponent. From these results, it works out the average expectation for the initial move and ranks them. This is the same as Snowie 2 ply. You can think of it as asking "what's my best move if I also consider every possible dice roll and move my opponent might make?"
For 2 ply (Snowie 3 ply), a similar process is done, but this time, not only are the opponents possible moves considered, but, for each of these, the player on roll's next move will be considered as well.
For a single move, on average there are about 20 legal moves to consider.
When doing a one ply analysis/evaluation, for the top n moves (from the move filter, GNU Backgammon needs to consider 21 rolls by the opponent, 20 and possible legal moves per roll) = 420 positions to evaluate.
Every additional ply will multiply the previous number of evaluations by about 400 odd, which explains the huge difference in playing speed/analysis speed between 0 ply and 2 ply settings. I don't think many people would enjoy playing against GNU Backgammon at 4 ply settings, where moves could take tens of seconds to be selected. Deeper lookahead than 2 ply actually gains relatively little in terms of playing strength and are not very interesting as settings for GNU Backgammon as an opponent or for rollouts (although 3 ply is quite fast on current computers). On the other hand, 4 ply analysis is reasonably fast on modern multi-cores machines.
First of all: There are several places in GNU Backgammon where you can adjust either it's skill at playing or the quality of it's hints and analysis:
→ → - choose Supremo or World Class. GNU Backgammon will take at most a few seconds choosing its moves and they will be very strong. At this setting, it is significantly stronger than any human player (on average, some classes of positions are evaluated less accurately).
→ - choose Supremo or World Class if you want hints to be accurate and fast. Anything lower doesn't really makes sense on current PCs.
→ - these settings are used by the Analyse Move/Game/Match or Session command. Note that this is totally different to what is used in the Hint command, which uses the above settings. You probably want at least Supremo here. A 7 point match will take at most 1 minute to analyse on the Supremo settings. This could be used to get immediate feedback after completing a match. An alternative is to use the more accurate 4 ply level. The same analysis would take maybe 15 minutes on a 4-cores computer and longer on more limited hardware. This would be more suitable to delayed, overnight for instance, processing of a batch of matches.
→ → tick the boxes for 'Cube decisions use same settings same as checker play' and 'Use same settings for both players'
→ → - select Expert here for fast rollouts or World Class for slower but more accurate ones. When doing rollouts, most of the time Expert play will be more than strong enough if you do say 1296 trials with no truncation. The rollout function has an enormous number of options, most of which are only useful when trying to investigate special positions. The simple Expert setting for both players is more accurate than any of the Analysis functions. The downside is that rolling out 1296 trials of an early move in a game can take from a couple of minutes at Expert level to hours at World Class or Supremo rollout settings.
A typical evaluation settings dialog is shown in this figure.
The dialog is consisting of two columns, the left column is for setting the checker play decision evaluation settings, and the right column is for setting the cube decision evaluation settings.
For each column you can select some predefined settings, or you can define your own settings.
In the lookahead box, you can adjust the lookahead of each evaluation by specifying the plies to be evaluated. Each ply costs approximately a factor of 21 in computational time. Also note that 2-ply is equivalent to Snowie's 3-ply setting.
In the box for Cubeful evaluations, you can specify if you want GNU Backgammon to evaluate the cube ownership in its evaluations. With this option turned on it generally improves the evaluation, specially when it's close to cube decisions, so we recommend that this option is turned on.
In the Noise box, you can add noise to the evaluation. This can be smart if you think the program plays to strong. You can use the Noise box option to introduce noise or errors in the evaluations. This is useful for introducing levels below 0-ply. The lower rated bots (e.g., BlunderBot on FIBS) use this technique. The introduced noise can be deterministic, i.e., always the same noise for the same position, or it can be random.
At the top of each evaluation settings column, it's possible to set a predefined setting.
Beginner This setting uses no lookahead and add up to 0.060 noise to the evaluation. With this setting GNU Backgammon will evaluate like a beginner.
Casual play This setting uses no lookahead and add up to 0.050 noise to the evaluation. With this setting GNU Backgammon will evaluate a bit better than the beginner setting but not much.
Intermediate This setting uses no lookahead and add up to 0.030 noise to each evaluation. It still plays a intermediate game.
Advanced This setting uses no lookahead and add up to 0.015 noise to each evaluation. This setting plays a good game.
Expert This setting uses no lookahead but does not add any noise to the evaluations. This settings play a strong game.
World class This setting uses 2-ply lookahead, it uses no noise and it uses a normal move filter. This plays a really strong game, on par with the very best humans players.
Supremo This is basically the same as the World Class setting, but it uses a larger move filter.
Grandmaster This setting uses 3-ply lookahead, no noise and a large move filter. This setting is extremely strong and still fast on current computers.
4ply This setting uses 4-ply lookahead, no noise and a large move filter. This setting is extremely strong, but it's also quite slow. It is more suitable to analysis than to actual play.
GNU Backgammon uses a technique called move filters in order to prune the complete list of legal moves when analysing checker play decisions.
A move filter for a given ply, say, 2-ply, consists of four parameters for each sub ply:
whether to analyse at all at this sub ply,
the number of moves always accepted at the given level,
the number of extra moves to add,
the threshold for adding extra moves.
A move filter for a given ply, say, 2-ply, consists of four parameters for each sub ply:
whether to analyse at all at this sub ply, the number of moves always accepted at the given level, the number of extra moves to add, the threshold for adding extra moves. For example, for 2-ply checker play decisions there are two move filters: one for pruning at 0-ply, and another for pruning at 1-ply. The predefined setting Normal has: accept 0 moves and add up to 8 moves within 0.16 at 0-ply, and no pruning at 1-ply.
Consider the opening position where 4-2 has been rolled:
GNU Backgammon starts by finding all possible moves and evaluate those at 0-ply:
| 1. | Cubeful | 0-ply | 8/4 6/4 | Eq.:+0.189 | |
| 2. | Cubeful | 0-ply | 24/20 13/11 | Eq.:+0.046 | (-0.143) |
| 3. | Cubeful | 0-ply | 13/11 13/9 | Eq.:+0.044 | (-0.145) |
| 4. | Cubeful | 0-ply | 24/22 13/9 | Eq.:+0.034 | (-0.155) |
| 5. | Cubeful | 0-ply | 24/22 24/20 | Eq.:-0.006 | (-0.194) |
| 6. | Cubeful | 0-ply | 24/18 | Eq.:-0.009 | (-0.198) |
| 7. | Cubeful | 0-ply | 24/20 6/4 | Eq.:-0.019 | (-0.208) |
| 8. | Cubeful | 0-ply | 13/9 6/4 | Eq.:-0.024 | (-0.213) |
| 9. | Cubeful | 0-ply | 13/7 | Eq.:-0.052 | (-0.241) |
| 10. | Cubeful | 0-ply | 24/20 8/6 | Eq.:-0.053 | (-0.242) |
According to the move filter the first 0 moves are accepted. The equity of the best move is +0.189, and according to the move filter we add up to 8 extra moves if they're within 0.160, that is, if they have equity higher than 0.029. Moves 5 through 18 all have equity lower that, so the move list after pruning at 0-ply consists of moves 1 through 4. According to the move filter we do not perform any pruning at 1-ply, so moves 1 through 4 are submitted for evaluation at 2-ply;
| 1. | Cubeful | 2-ply | 8/4 6/4 | Eq.:+0.180 | |
| 2. | Cubeful | 2-ply | 24/20 13/11 | Eq.:+0.052 | (-0.127) |
| 3. | Cubeful | 2-ply | 13/11 13/9 | Eq.:+0.043 | (-0.137) |
| 4. | Cubeful | 2-ply | 24/22 13/9 | Eq.:+0.035 | (-0.145) |
| 5. | Cubeful | 0-ply | 24/22 24/20 | Eq.:-0.006 | (-0.185) |
| 6. | Cubeful | 0-ply | 24/18 | Eq.:-0.009 | (-0.189) |
| 7. | Cubeful | 0-ply | 24/20 6/4 | Eq.:-0.019 | (-0.199) |
| 8. | Cubeful | 0-ply | 13/9 6/4 | Eq.:-0.024 | (-0.203) |
| 9. | Cubeful | 0-ply | 13/7 | Eq.:-0.052 | (-0.232) |
| 10. | Cubeful | 0-ply | 24/20 8/6 | Eq.:-0.053 | (-0.232) |
If we instead request a 4-ply checker play decision, GNU Backgammon will use the move filters defined for 4-ply:
| Ply | Accept moves | Extra moves | Threshold for extra moves |
| 0 | 0 | 8 | 0.160 |
| 1 | no pruning | ||
| 2 | 0 | 2 | 0.040 |
| 3 | no pruning |
The 4-ply move filter is identical to the 2-ply for pruning at 0-ply, so after 0-ply we have the same three moves as above. Since there is no pruning at 1-ply these three moves are evaluated at 2-ply as above. There is no pruning at 3-ply.
At 4-ply we do not accept any moves, but add up to two moves if there within 0.040 from the best move. Since the second best move is -0.138 worse than the best move, we do not accept any moves to be evaluated at 4-ply. Hence GNU Backgammon will actually not evaluate any moves on 4-ply.
The predefined move filters all have accept 0 moves, in order to facilitate fast decisions and analysis, i.e., no need to waste much time over obvious moves.
For post-mortem analysis it may be worthwhile to ensure that GNU Backgammon analyses at least two moves at the specified ply. To do this, specify accept 2 moves in the move filters you use for analysis. However, do note that GNU Backgammon will force evaluation at the specified ply if the actual move made is doubtful. This ensures that all errors and blunders are evaluated at the same level.
The move filter allows you to control exactly how many moves GNU is examining at each ply. A ply is basically one move played by one side, thus if both sides played a move, it would be one whole move, but two plies, one for each side. To change the specific settings, press the Modify... button.
Although the predefined levels, such as World Class, Supremo, etc. are tested and good, you may want to know or control how GNU filters its moves to analyse and how many.
If you are playing Expert level or another 0-ply setting, the Move Filter settings will not change a thing, as Expert level automatically examines all moves. At Supremo level, this changes though, as it takes a selection of the best moves from 0-ply and examines them at 2-ply. This means that for those selected moves it will calculate all the possibilities 2 plies ahead and evaluate them, allowing it to find better moves. Since Supremo is a 2-ply setting, we are only interested in the 2-ply settings of Large as in the figure above. 3-ply or 4-ply settings will have no effect here because Supremo doesn't examine at that depth.
In the figure above, we can see it first will Always accept 0 moves. This first line means that it won't force any moves to be analysed at 2-ply, it will only analyse moves according to the second line. If it had said it would always analyse 2 moves, this would mean that no matter how ridiculously bad the 2nd move was compared to the 1st, it would analyse both at 2-ply.
The second line says it will Add extra 16 moves within 0.320. This means that provided they aren't more than 0.320 equity worse than the top move, it will select a maximum of 16 moves to analyse at 2-ply. For example, in the figure below, the 2nd best move is no less than 0.453 equity worse than the top choice, so it didn't bother analysing them at 2-ply as it is unlikely to change its mind on what the best move is.
Take a look at next figure.
Here, the exact same settings were maintained, but the 1-ply filter was activated. This just means that those 16 moves selected from the 0-ply are sent instead to be analysed at 1-ply, and then up to 5 moves from 1-ply will be sent to be analysed at 2-ply. So this would actually be faster than the previous setting (and weaker), since a maximum of only 5 moves would be analysed at 2-ply depth.
Tip: Feel free to experiment with the settings, as you can always reset them by simply choosing one of the predefined levels. In order to see if they are better, or as good but faster, I'd suggest comparing the results with Supremo. One setting I have that works quite well, is to take the basic Supremo setting and in the Move filter reduce the 16 to 12. It cuts down on the thinking time by 20-25% more or less, and I haven't seen more than one case in over 10,000 moves where it missed the best move.
In the evaluation settings dialog box you can specify whether or not checker play should be evaluated cubeful. It's recommended that you use cubeful evaluation. To get an understanding of what cubeful checker play evaluations are, you can take a look at this position:
In this position black has rolled 51 and he has a good position. If the position is evaluated cubeless the best move is 13/7. Black can hope white does not roll 34 or 35 form the bar and has now a good chance to close white out in the next few rolls. However if white rolls one of the four hitting numbers from the bar, white will quite soon have a really hot redouble. This redouble increases whites equity so much that black actually should play this move safe. He should play 13/8 6/5. However if the evaluation was set to cubeless, an setting which assumes white will never redouble, black should play 13/8.
Here's another example:
This is from a 5 point match where black has 1 point and white has 3 points. Black wins the opening roll and considers playing 13/11 6/5 or 24/23 13/11.
If GNU Backgammon uses a cubeless evaluation it will play 24/23 13/11. But if you're using a cubeful evaluation it will play 13/11 6/5. Slotting with 6/5 is at this score a better move even though it loses more gammons. The gammons black are losing won't matter anyway, since black will turn the cube in the next few rolls anyway. The slotting play also wins more gammons, and with the cube tuned to 2, black should play towards gammonish positions at this score.
You can read more about cubeful evaluations in the [[Appendix]].
It's recommended that you use cubeful checker evaluations.
A feature in the evaluation is the use of a set of neural networks just to prune away move candidates within a deeper ply search. This increases the speed considerably and it doesn't lose much playing strength compared to evaluation without these pruning neural nets. Jim Segrave did an analysis of this and found that less than 1% of all moves come out different with the pruning nets activated. In most of these positions the move would not have made any difference to the game at all.
If you think GNU Backgammon plays too strong for you, you can add some noise to its evaluation. The number you add into the field in the evaluations setting is the limit amount of noise that will be added to the evaluation.
If noise is added to the evaluations GNU Backgammon will take a Box Müller transform of a point in the unit circle and add to each possible outcome probability. This means that the addition is random, but distributed so that it's more likely to have an noise addition close to zero than a noise addition close to the limit. The noise addition is limited to the number you put into the noise field in the dialog box.
If you check the box Deterministic noise, the noise added to each evaluation will be based on a sum of the bytes in the hash of the board position, which (by the central limit theorem) should have a normal distribution. In that way you will always have that same noise amount to a position, since the noise added to the evaluation is only depending on the position itself.
If you want GNU Backgammon to evaluate and play as strong as possible, you should not add any noise.
You can change the appearance of GNU Backgammon. There is a lot of options to choose among and you can have the board look like nearly anything. This section will help you through some on the appearance customization.
To change the look of the board, you should click → . This will open a dialog box like this:
In this dialog box you see a preview picture of the board at the right side, and you have notebook with options to the left.
There are two different board rendering engines in GNU Backgammon. It's a 2 dimensional rendering engine which is simple and fast, but still makes really good board images. The moves can be animated.
The other board rendering type is a 3 dimensional board engine based on OpenGL. This board rendering engine makes astonishing fine board graphics, and animates the rolls and moves beautifully. You can even add textures to your boards and checkers. However, the 3D rendering type need a good modern graphic card which can take 3D hardware acceleration.
The leftmost tab in the appearance settings notebook is the General option. You can here select between the 2D board or the 3D board. You can also choose between different other settings. Most of the settings here are self explanatory.
GNU Backgammon is supplied with a program makebearoff that is used to generate bearoff databases. Due to various limitations it is only possible to generate bearoff databases with a size less than 2GB, i.e., the 13pt one-sided database and the 11 checker two-sided database are the largest databases that can be generated with makebearoff.
On current (2014) hardware the creation of the 11 checker two-sided database will take a few hours. It is approximately 3 times longer for each additional checker or each additional point.
To generate one sided database issue
makebearoff -o 10 -f gnubg_os.bd
to generate the one sided 10 point database. The program makebearoff uses a cache to store previously generated positions. You may set the cache size with the -s size option, e.g.,
makebearoff -o 10 -s 123456789 -f gnubg_os.bd
to use 123,456,789 bytes of memory for cache size. In general, if the cache size is less than the size of the database to be generated, then extra time is needed to generate the bearoff database because some positions may have to be calculated several times.
makebearoff can also reuse previously generated databases, so if you already had generated the 9 point database you can reuse it:
mv gnubg_os.bd gnubg_os9.bd
makebearoff -o 10 -O gnubg_os9.bd -f gnubg_os.bd
Note that makebearoff requires temporary disk space to generate both one sided and two sided databases. In general, twice the disk space of the database to be generated is needed.
To generate a two sided database issue
makebearoff -t 6x8 -f gnubg_ts.bd
This example will generate the 8 checkers on 6 points database. Again, it's possible to adjust the amount of memory with the -s option. It's recommended to set the cache size to the maximum amount of memory available (although there is no need to set it beyond the size of the bearoff database to be generated).
Other options for makebearoff are available, see makebearoff --help for the complete set.
The accompanying program makehyper is used to generate databases for Hypergammon. For example, to generate the 3-checker database issue the command
makehyper -c 3 -f hyper3.bd
Since the generation can be time consuming, makehyper will generate a checkpoint file (in the example above: hyper3.bd.tmp) that can be used to restart the calculation if needed by using the -r option. You can also change the default convergence threshold of 0.00001 if you're happy with less accurate equities. To generate the 3 checker database you need approximately 400 MB of free memory. On current (2014) hardware the calculation for the 3-checker database will take a few hours (1- and 2-checker are much faster).
See makehyper --help for the complete set of available options.
You may download the two sided database with 6 checkers on 6 points from https://alpha.gnu.org/gnu/gnubg/gnubg_ts0.bd.gz and the one sided database with 15 checkers 6 points from https://alpha.gnu.org/gnu/gnubg/gnubg_os0.bd.gz.
Larger databases are available for download from https://dl.xs4all.nl/Museum/Demon/games/gnubg/databases/.
The databases's installation directory depends on where GNU Backgammon is installed on your system. It is displayed by → → .
To verify that your generated or downloaded bearoff database is correct, the table below lists the MD5 checksums for a number of possible databases.
The table below contains the MD5 checksums for the compressed one sided bearoff databases, i.e., databases generated with default options.
| Checkers | Points | MD5 checksum |
| 15 | 1 | c789f049ec98ce4e307b471257999f39 |
| 15 | 2 | b6e61c1625ae4b3b164e93ab064192b9 |
| 15 | 3 | 346dae6139ccb4b227c534373e5c52e4 |
| 15 | 4 | 653255f5f9f22fd50277f7ff25b2a343 |
| 15 | 5 | 2064f9a56b23117d053a573c96a92fa2 |
| 15 | 6 | 3dc7b833c4670849cee00479a9e21b49 |
| 15 | 7 | 67235c8e0ee152df5daf36cbeae5b3c2 |
| 15 | 8 | a4acbb5c7e9e1f08e561afe0af934e5c |
| 15 | 9 | 9c4ddab4e51c3e668c9c97b8f8768dbc |
| 15 | 10 | 81b3898f06bbd08ee8295a839251a10a |
| 15 | 11 | 78ecb4be86dab6af8755ea4063d50fb6 |
| 15 | 12 | 770fcff48894a96ebb2249343ef94866 |
| 15 | 13 | cc74b69a62f6e648936f533838a527a8 |
| 15 | 14 | not available |
| 15 | 15 | not available |
| 15 | 16 | not available |
| 15 | 17 | not available |
| 15 | 18 | not available |
The table below contains the MD5 checksums for the default two sided bearoff databases.
| Checkers | Points | MD5 checksum |
| 1 | 6 | 7ed6f8e7fce16ea2b80e07a4a516653c |
| 2 | 6 | e9d760bf213841c285245ed757a52f4d |
| 3 | 6 | 9d67da3db32ad4720cc38eecf9a67967 |
| 4 | 6 | 9156f37032d1d4b0352a41186e632dfc |
| 5 | 6 | 0db19ab08feae1feb33ddbd709479f62 |
| 6 | 6 | 44b6040b49b46cb9dd2ce8caa947044d |
| 7 | 6 | 9eb8b042d4d2ddf8d40e74a892745ad5 |
| 8 | 6 | fcdbbc80b7ef84ddc81b839d0f26bed1 |
| 9 | 6 | a11b2d410d51401143d05e73f9ffac15 |
| 10 | 6 | 12dc70c86f356d06bc96ee38dee40c62 |
| 11 | 6 | 68a0fa972bdde7b14a6b911d1dc80a30 |
| 12 | 6 | not available |
| 13 | 6 | not available |
| 14 | 6 | not available |
| 15 | 6 | not available |
As the generation of the Hypergammon databases are an iterative process it's not possible to give MD5 checksum for these, as it depend heavily on your convergence threshold, the number of restarts, and rounding errors.
A random position from the database is found in Example 2, “Random position from hypergammon database”. The equities and percentages in your own database should be very similar (if not identical):
GNU Backgammon Position ID: ADAAAQAkIAAAAA
Example 2. Random position from hypergammon database
GNU Backgammon Position ID: ADAAAQAkIAAAAA
Match ID : cAkAAAAAAAAA
+13-14-15-16-17-18------19-20-21-22-23-24-+ O: gnubg
| X X | | X | 0 points
| | | |
| | | |
| | | |
| | | |
v| |BAR| | (Cube: 1)
| | | |
| | | |
| | | |
| O | | | On roll
| O | | O | 0 points
+12-11-10--9--8--7-------6--5--4--3--2--1-+ X: jth
Player Opponent
Position 3018 2831
Owned cube : -0.0230
Centered cube : -0.2310
Centered cube (Jacoby rule) : -0.2186
Opponent owns cube : -0.3548
Win W(g) W(bg) L(g) L(bg) Equity (cubeful)
static: 0.456 0.244 0.014 0.318 0.019 (-0.168 (-0.219))
No double : -0.219
Double, pass : +1.000 (+1.219)
Double, take : -0.710 (-0.491)
Correct cube action: No double, beaver
Multiple match equity tables are bundled with GNU Backgammon, although most of them are only of marginal or historical interest.
- Rockwell-Kazaross or Kazaross-XG2 are the recommended choice. They were created by rolling out the initial position for every score up to -15:-15 and are the best currently available estimations of the match equities for a strong bot playing itself.
- g11, snowie and woolsey are the tables that were used by earlier versions of GNU Backgammon, Snowie or for hand calculations back when bots didn't do match equity calculations (or there was no bot at all). All of them are now considered obsolete. Analyses or rollouts using them can still be found in books, magazines or web sites so it can occasionally be interesting to use them in GNU Backgammon for comparison to these older results.
- jacobs, jac050 and jac100 are from the book _Can a Fish Taste Twice as Good_ by Jake Jacobs and Walter Trice and give match equities if players are of equal strength, if one is 50 Elo points stronger and if one is 100 points stronger respectively. They should only be used to analyse such unequal opponents situations.
- The other tables are obsolete and of no practical use.
Accessing the GNU Backgammon Python shell
To access the Python shell, either type `>' from the command line or select → from the GUI.
board()
command(cmd)
evaluate()
evalcontext()
eq2mwc()
mwc2eq()
cubeinfo()
met()
positionid()
positionfromid()
positionkey()
positionfromkey()
positionbearoff()
positionfrombearoff()
navigate([next=N,[game=N]])
Match navigation.
Without any arguments, go to first move of first match.
With next == N, move forward N game records.
With game == N, move forward/backward N games.
Navigate never wraps around.
On success, returns None. If unable to complete the requested number of moves, returns a pair of (next-remaining,game-remaining).
match([analysis=1/0, boards=1/0, statistics=0/1, verbose=0/1])
Return the current match. For example,
> m = gnubg.match()
Takes the following optional keyword arguments:
analysis
When 0, discard analysis data. default is 1.
boards
When 1, add current board to move/double records. Default is 1.
statistics
When 1, include game and match statistics. Default is 0.
verbose
When 1, include derived analysis values. Default is 0.
gnubg.match() returns a dictionary containing the following items:
match-info
General match info
games
A sequence, one element per game.
stats (optional)
Match statistics.
A dictionary containing the following items:
match-length
variation
One of Standard,Nackgammon, Hypergammon1, Hypergammon2 or Hypergammon3.
rules (optional)
Additional rules used. A subset of NoCube, Crawford and Jacoby.
X
O
Per player information. Each a dictionary containing rating and name.
annotator (optional)
round (optional)
place (optional)
date (optional)
Sequence of (Day,Month,Year).
event (optional)
default-eval-context
Default evaluation context. A dictionary in the same format as returned by evalcontext().
default-rollout-context
Default rollout context.
Example,
>>> m['match-info']
{'match-length': 25, 'rules': ('Crawford',), 'default-eval-context': {'plies': 2, 'deterministic': 1, 'noise': 0.0, 'cubeful': 1}, 'annotator': 'GNU 0.14', 'O': {'rating': '0 (Exp 0)', 'name': 'Moshe Tissona'}, 'round': 'Final', 'place': 'Monte Carlo', 'variation': 'Standard', 'default-rollout-context': {'n-truncation': 11, 'initial-position': 0, 'trials': 0, 'stop-on-std': 0, 'variance-reduction': 1, 'late-eval': 0, 'truncated-rollouts': 0, 'truncate-bearoff2': 1, 'cubeful': 1, 'truncate-bearoffOS': 1, 'seed': 1177750272, 'quasi-random-dice': 1, 'minimum-games': 144}, 'date': (13, 7, 2003), 'X': {'rating': '0 (Exp 0)', 'name': 'Jon Royset'}, 'event': 'World Championship 2003'}
A dictionary containing the following items:
info
General game info. For example,
>>> m['games'][0]['info']
{'points-won': 1, 'score-X': 0, 'score-O': 0, 'winner': 'X', 'resigned': False}
If no winner is specified, winner is None.
>>> m['games'][2]['info']
{'score-X': 2, 'winner': None, 'score-O': 0}
game
A Sequence of actions.
stats (optional)
Game statistics. Similar entries to → from the GUI.
GNU Backgammon works with many different kinds of equities. The equity is defined as the expected value of the position. However, this value can be expressed in several different metrics and may be calculated with or without taking the effect of the cube into consideration. In the following section we will describe the equities used and calculated by GNU Backgammon.
This is the value of the position in money game, e.g., if your equity is +0.4 an you are playing money game with a $1 stake, you will win $0.40 on average. The money equity can be calculated with or without taking the effect of the doubling cube into consideration, or cubeful or cubeless. The cubeless equity can be calculated from the basic formula: 2*p(w)-1+2(p(wg)-p(lg))+3(p(wbg)-p(lbg)). Evaluating the cubeful equity is much more difficult; it can either be estimated from the cubeless equity by using transformations as outlined by Rick Janowski or by constructing a neural net that directly outputs cubeful equities. GNU Backgammon uses the former approach (the section called “Cubeful equities”).
In match play we're generally not particular interested in the outcome of the individual games as much as the outcome of the entire match, so the interesting quantity for match play is match winning chance (MWC). As for the money equity the MWC can be calculated with and without the effect of the doubling cube. The MWCs are generally calculated with the use of a match equity table, which contains the chance of winning the match before a game starts, e.g., if the score is 0-0 in a 1pt match each player has 50% chance of winning the match before the game starts assuming they're of equal skill.
The cubeless MWC is calculated as: MWC(cubeless) = p(w) * MWC(w) + p(l) * MWC(l) + p(wg) * MWC(wg) + p(lg) * MWC(lg) + p(wbg) * MWC(wbg) * p(lbg) * MWC(lbg).
For example, if the w/g/bg distribution is 0 30 60 - 40 10 0 and the match score is 1-3 to 5 with the cube on 2 the cubeless MWC is:
MWC(cubeless)= 30% * 50% + 30% * 0% + 30% * 100% + 10% * 0% + 0% * 100% + 0% * 0% = 45%,
so the cubeless MWC is 45%.
Evaluating the cubeful MWC is more difficult, and as for the cubeful money equity it's possible to estimate cubeful MWCs from transformation on the w/g/bg distribution or directly calculate it from neural nets. GNU Backgammon uses the former approach, but the formula are currently not published.
It's generally very difficult to compare MWCs. For example, it's hardly worth mentioning a 0.5% MWC error at DMP where as it's a huge error at 0-0 to 7. It is therefore of interesting to normalize the MWCs to some common scale. The most often used normalization is Normalized Money Game Equity (NEMG) where the MWC for any game is transformed into the same interval as money game, i.e., -3 to +3 (due to anomalies at certain match scores the NEMG can go below -3 and above +3). The transformation is linear:
NEMG = 2 * (MWC-MWC(l))/(MWC(w)-MWC(l)) - 1
In other words, extrapolation with the following two extrapolation points: (MWC(w),+1) and (MWC(l),-1).
For example, suppose the score is 3-1 to 5 with the cube on 2: MWC(l)=0% and MWC(w)=50%:
| MWC | NEMG |
| 0% | -1 |
| 25% | 0 |
| 50% | +1 |
| 75% | +2 |
| 100% | +3 |
Note that a w/g/bg distribution of 0 100 100 - 0 0 0 gives a NEMG of +3 whereas the corresponding money equity is only +2. This is because the gammon price is high for that particular score. When both players are far from winning the match, e.g., 0-0 to 17 or 1-0 to 17, NEMG is very close to the usual money equity.
NEMG can be calculated from both cubeless and cubeful MWCs.
A word of caution: A cubeless NEMG calculated from a cubeless MWC could be named cubeless equity, but in most backgammon literature this term seems to be reserved for the cubeless money equity.
This chapter is a brief description of how GNU Backgammon calculates cubeful equities. The formula build directly on the work by Rick Janowski Take-Points in Money Games from 1993.
The basic formula for cubeful equities as derived by Janowski is
E(cubeful) = E(dead) * (1-x) + E(live) * x,
where E(dead) is the dead cube equity (cubeless equity) calculated from the standard formula. E(live) is the cubeful equity assuming a fully live cube. We'll return to that in the next section. x is the cube efficiency. x=0 gives E(cubeful)=E(dead) as one extreme and x=1 gives E(cubeful)=E(live) as the other extreme. In reality x is somewhere in between, which typical values around 0.6 - 0.8.
Janowski's article doesn't mention cubeful equities, so we use the straightforward generalization
MWC(cubeful) = MWC(dead) * (1-x) + MWC(live) * x.
as MWC is the entity that is used for match play evaluations.
The live cube equity is the equity assuming that the equity changes continuously, so that doubles and takes occurs exactly at the double point and take point. For gammon-free play this is the well-known take point of 20%. Janowski derives the more general formula
TP = (L-0.5)/(W+L+0.5)
where W is the average cubeless value of games ultimately won, and L is the average cubeless value of games ultimately lost. For example, for the following position
GNU Backgammon evaluates
| Win | W(g) | W(bg) | L(g) | L(bg) | |
| static: | 0.454 | 0.103 | 0.001 | 0.106 | 0.003 |
and hence W=(0.454 + 0.103 + 0.001)/0.454=1.229 and L=(0.556+0.106+0.003)/0.556) = 1.196. For gammon-free positions, e.g., a race, W=1 and L=1.
The live cube equity is now based on piecewise linear interpolation between the points (0%,-L), (TP,-1), (CP,+1), and (100%,+W): if my winning chance is 0 I lose L points, at my take point I lose 1 point, at my cash point I cash 1 point, and when I have a certain win I win W points:
For match play there is no simple formula, since redoubles can only occur a limited number of times.
The live cube take point is generally calculated as
TP(live, n Cube)=TP(effective, n cube) * (1 - TP(live, 2n cube))
So to calculate the live cube take points for a 1-cube at 3-0 to 7 we need the live cube take points for the 4-cube and the 2-cube. For the position above and using Woolsey's match equity table the live cube take point are:
| Cube value | TP for Black | TP for White |
| 4 | 0% | 41% |
| 2 | 15% | 38.5% |
| 1 | 24.5% | 27.3% |
The calculation of these are left as an exercise to the reader.
Ignoring backgammons, the gammon rates for White and Black are 0.106/54.6=19% and 0.103/0.454=22%, respectively. If White wins the game his MWC will be
81% * MWC(-3,-7) + 19% * MWC(-2,-7) = 78%
and if Black wins his MWC will be
78% * MWC(-4,-6) + 22% * MWC(-4,-5) = 41%.
If White cashes 1 point he has MWC(-3,-7)=76% and if Black cashes he has MWC(-4,-6)=36%. Analogous to money game the live cube MWC is calculated as piecewise linear interpolation between (0%,22%), (24.5%,24%), (72.7%,36%), and (100%,41%) (from black's point of view):
Having established the live cube equities and MWCs we're now in position to calculate the 0-ply cubeful equities.
Let's start with money game: the cubeless equity is -0.097 and the live cube equity can be determined from the figure above as -0.157. Thus, the cubeful equity is -0.138.
For the match play example at the score 3-0 the cubeless MWC is 29.1% and from the figure Black using wins=45.4% we can determine the live cube MWC to be 29.2%. Using a value of x=0.68 we arrive at a cubeful MWC of 29.17%.
The previous section concerned the calculation of 0-ply cubeful equities, so how so GNU Backgammon calculate cubeful 2-ply equities? The answer is: by simple recursion:
Equity=0
Loop over 21 dice rolls
Find best move for given roll
Equity = Equity + Evaluate n-1 ply equity for resulting position
End Loop
Equity = Equity/36
Note that evaluating the n-1 ply equity involves a cube decision, since the opponent may double, so GNU Backgammon will actually calculate the two n-1 ply equities: (a) assuming no double, and (b) assuming double, take. These two equities are combined with the equity for a pass, and the optimum of these three is added to the resulting equity. For a cubeful 2-ply evaluation GNU Backgammon will end up calculating the following cubeful 0-ply equities: centered 1-cube, opponent owns 2-cube, owned 4-cube, and opponent owns 8-cube.
Note that the 2-ply level does not use the cube efficiency, it's not used until at the 0-ply level, but it's possible to calculate an effective one by isolating x in the basic cube formula:
x(eff) = (E(2-ply cubeful) - E(2-ply dead))/(E(2-ply live)-E(2-ply dead)).
The cube efficiency is obviously an important parameter, unfortunately there haven't been much investigation carried out, so GNU Backgammon basically uses the values 0.6-0.7 originally suggested by Rick Janowski:
| Position Class | x (Cube efficiency) |
| Two-sided (exact) bearoff | n/a |
| One-sided bearoff | 0.6 |
| Crashed | 0.68 |
| Contact | 0.68 |
| Race | linear interpolation between 0.6 and 0.7 |
For race GNU Backgammon uses linear interpolation based on pip count for the player on roll. A pip count of 40 gives x=0.6 and 120 gives x=0.7. If the pip count is below 40 or above 120 values of x=0.6 and x=0.7 are used, respectively.
For the two sided bearoff positions the cubeful money equity is already available from the database, so for money game there is no need to calculate cubeful equities via Janowski's formula. However, the cubeful equities for money game cannot be used for match play. Instead of using a fixed value of x, say, 0.6, GNU Backgammon will calculate an effective value based on the cubeful money equity. The cubeful MWC is calculated as usual, but with the calculated x.
There is obviously room for improvements. For example, holding games should intuitively have a lower cube efficiency, since it's very difficult to double effectively: either it's not good enough or you've lost the market by a mile after rolling a high double or hitting a single shot. Similarly, backgames will often have a low cube efficiency, whereas blitzes have may have a higher cube efficiency.
GNU Backgammon's cube decisions are simple based on calculations of cubeful equities. For a double decision GNU Backgammon calculates the cubeful equity for no double and the cubeful equity for double, take. Combined with the equity for double, pass, it's possible to determine the correct cube action.
The figure below shows the relevant cubeful equities for White and black's cube decisions in sample position from earlier.
On 0-ply Black will double when the green curve (White owns 2-cube) is above the red curve (centered cube), and White will take as long as the green curve is below 1. Similarly, White will double when the blue curve (Black owns 2-cube) is below the red curve (centered cube), and Black takes as long as the blue curve is above -1.
Note that GNU Backgammon doesn't calculate the take point or double point explicitly. The cube decision is simply made by comparing equities from the figure.
Janowski has developed two other models for cubeful equities. The first is a generalization of the one used by GNU Backgammon; it introduces two cube efficiencies instead of one. Often you may see that the cube efficiencies are different for the two players, and the refined general model as it is named by Janowski, tries to take this into consideration by using different cube efficiency parameters for the two players. For example, the blitzer may have another cube efficiency that the blitzee.
The second model is not published, but redefines the cube efficiency into a value that can be understood more intuitively and calculate easily from rollouts.
This section describes a method for compactly recording a backgammon position. It demonstrates how to encode a position into 10 binary bytes, which is useful for minimizing the space used when recording large numbers of positions in memory or on disk. There is also an ASCII representation in 14 characters, which is convenient for output to the screen, for copying and pasting to transfer positions between programs which support the format, and for communicating positions via Usenet news or e-mail. The 10 byte binary format is called the key, and the 14 character ASCII format is the ID.
The key is essentially a bit string (imagine you start with an empty sequence of bits, and continue adding either 0 or 1 to the end). The way to build up a sequence that corresponds to a given position is:
For every point around the board (starting at the ace point of the player not on roll, continuing around to the 24 point and ending at the bar):
append as many 1s as the player not on roll has checkers on that point (if any).
append a 0.
For every point around the board (starting at the ace point of the player on roll, continuing around to the 24 point and ending at the bar):
append as many 1s as the the player on roll has checkers on that point (if any).
append a 0.
Pad out the string to 80 bits with 0s.
The worst-case representation will require 80 bits: you can see that there are always 50 0 bits even if there are no checkers at all. Each player has a maximum of 15 checkers in play (not yet borne off) which require a 1 bit wherever they are positioned. That's 30 bits to take of all checkers, plus the 50 bits of overhead for a total of 80 bits (the last bit is always 0 and isn't strictly necessary, but it makes the code slightly easier). This bit string should be stored in little-endian order when packed into bytes (i.e. the first bits in the string are stored in the least significant bits of the first byte).
As an example, here's what the starting position looks like in the key format:
| 0 0 0 0 0 | opponent has no checkers on his ace to 5 points |
| 11111 0 | 5 checkers on the 6 point |
| 0 | empty bar |
| 111 0 | 3 on the 8 |
| 0 0 0 0 | no others in his outfield |
| 11111 0 | 5 on the midpoint |
| 0 0 0 0 0 | none in our outfield |
| 0 0 0 0 0 | or in our board, until... |
| 11 0 | two on the 24 point |
| 0 | none on the bar |
| 0 0 0 0 0 | player on roll has no checkers on his ace to 5 points |
| 11111 0 | 5 checkers on the 6 point |
| 0 | empty bar |
| 111 0 | 3 on the 8 |
| 0 0 0 0 | no others in his outfield |
| 11111 0 | 5 on the midpoint |
| 0 0 0 0 0 | none in opponent's outfield |
| 0 0 0 0 0 | or in opponent's board, until... |
| 11 0 | two on the 24 point |
| 0 | none on the bar |
so altogether it is:
00000111110011100000111110000000000011000000011111001110000011111000000000001100
In little endian bytes it looks like:
| 11100000 | 01110011 | 11110000 | 00000001 | 00110000 | 11100000 | 01110011 | 11110000 | 00000001 | 00110000 |
| 0xE0 | 0x73 | 0xF0 | 0x01 | 0x30 | 0xE0 | 0x73 | 0xF0 | 0x01 | 0x30 |
so the 10 byte key (in hex) is E0 73 F0 01 30 E0 73 F0 01 30.
The ID format is simply the Base64 encoding of the key. (Technically, a Base64 encoding of 80 binary bits should consist of 14 characters followed by two = padding characters, but this padding is omitted in the ID format.)
To continue the above example, splitting the 10 8-bit bytes into 14 6-bit groups gives:
111000 000111 001111 110000 000000 010011 000011 100000 011100 111111 000000 000001 001100 000000
In Base64 encoding, these groups are respectively represented as:
4 H P w A T D g c / A B M A
So, the position ID of the checkers at the start of the game is simply:
4HPwATDgc/ABMA
You can set the board in GNUbg either by writing the position ID into the position text input field in the GUI or by executing the command
set board 4HPwATDgc/ABMA.
Notes
This encoding is obviously not as compact as it could be: in particular, there are lots of redundant representations of illegal positions where both players have checkers on the same point. Theoretically, it would be possible to get it down to 64 bits by using Walter Trice's D() expressions, but I think you'd have to be a mathematical masochist to try it!
Thanks to Tom Keith and David desJardins for their suggestions on simplifying the encoding without increasing the worst case length.
This section describes how the match ID is calculated. The match ID can be used for easy exchange of positions for GNUbg users in conjunction with the position ID. The match key is a 9 byte representation of the match score, match length, value of cube, owner of cube, Crawford game flag, player on roll, player to make a decision, doubled flag, resigned flag, and the dice rolled. The match ID is the 12 character Base64 encoding of the match key. Match key
The match key is a bit string of length 66:
| 1-4 | 5-6 | 7 | 8 | 9-11 | 12 | 13 | 14-15 | 16-18 | 19-21 | 22-36 | 37-51 | 52 |
| Cube | CubeOwner | DiceOwner | Crawford | GameState | TurnOwner | Double | Resign | Dice1 | Dice2 | MatchLen x 15 | Score1 x 15 | Score2 x 15 |
Bit 1-4 contains the 2-logarithm of the cube value. For example, a 8-cube is encoded as 0011 binary (or 3), since 2 to the power of 3 is 8. The maximum value of the cube in with this encoding is 2 to the power of 15, i.e., a 32768-cube.
Bit 5-6 contains the cube owner. 00 if player 0 owns the cube, 01 if player 1 owns the cube, or 11 for a centered cube.
Bit 7 is the player on roll or the player who did roll (0 and 1 for player 0 and 1, respectively).
Bit 8 is the Crawford flag: 1 if this game is the Crawford game, 0 otherwise.
Bit 9-11 is the game state: 000 for no game started, 001 for playing a game, 010 if the game is over, 011 if the game was resigned, or 100 if the game was ended by dropping a cube.
Bit 12 indicates whose turn it is. For example, suppose player 0 is on roll then bit 7 above will be 0. Player 0 now decides to double, this will make bit 12 equal to 1, since it is now player 1's turn to decide whether she takes or passes the cube.
Bit 13 indicates whether an doubled is being offered. 0 if no double is being offered and 1 if a double is being offered.
Bit 14-15 indicates whether an resignation was offered. 00 for no resignation, 01 for resign of a single game, 10 for resign of a gammon, or 11 for resign of a backgammon. The player offering the resignation is the inverse of bit 12, e.g., if player 0 resigns a gammon then bit 12 will be 1 (as it is now player 1 now has to decide whether to accept or reject the resignation) and bit 13-14 will be 10 for resign of a gammon.
Bit 16-18 and bit 19-21 is the first and second die, respectively. 0 if the dice has not yet be rolled, otherwise the binary encoding of the dice, e.g., if 5-2 was rolled bit 16-21 will be 101-010.
Bit 22 to 36 is the match length. The maximum value for the match length is 32767. A match length of zero indicates that the game is a money game.
Bit 37-51 and bit 52-66 is the score for player 0 and player 1 respectively. The maximum value of the match score is 32767.
For example, assume the score is 2-4 in a 9 point match with player 0 holding a 2-cube, and player 1 has just rolled 52. The match key for this will be (note that the bit order is reversed below for readability)
1000 00 1 0 100 1 0 00 101 010 100100000000000 010000000000000 001000000000000
In little endian the bytes looks like:
01000001 10001001 00101010 00000001 00100000 00000000 00100000 00000000 00
0x41 0x89 0x2A 0x01 0x20 0x00 0x20 0x00 0x00
Analogous to the position ID from the previous section the match ID format is simply the Base64 encoding of the key.
To continue the example above, the 9 8-bit bytes are grouped into 12 6-bits groups:
010000 011000 100100 101010 000000 010010 000000 000000 001000 000000 000000 000000
In Base64 encoding, the groups are represented as:
Q Y k q A S A A I A A A
So, the match id is simply:
QYkqASAAIAAA
If someone post a match ID you can set up the position in GNUbg by writing or pasting it into the Match ID text input field on the main window, or by executing the command
set matchid QYkqASAAIAAA.
As mentioned above GNU Backgammon writes a CSS style sheet along with the generated XHTML file. The CSS style sheet may be written verbatim in the header section of the XHTML file, to an external file named gnubg.css, or inside the tags using the style attribute. If you wish to make any modifications to the style sheet without modifying the actual source code of GNU Backgammon you have to choose one of the first two methods. Note that the special export for BGonline / GammOnLine uses the third method since the XHTML is pasted into a web page without the possibility to modify the header section of the page where the style sheet is defined. Thus, it's not possible to modify the style of this variant of generated XHTML without modifications of the source code or extensive search and replace in the generated XHTML.
Below follows a description of the CSS classes used in the XHTML export:
| Class | Description |
| .movetable | Style applied to the entire table used for the move analysis |
| .moveheader | The header of the move analysis table |
| .movenumber | The rank number of a move in the move analysis |
| .moveply | The column indicating the number of plies or rollout |
| .movemove | The formatted move, e.g., 13/7 8/7. |
| .moveequity | The column with the equity or MWC. |
| .movethemove | Special style for row that contains the actual move chosen by the player |
| .moveodd | Special style for the odd rows. Can be used to give an alternating color for the rows. |
| .percent | Style for the game winning probabilities and equities in the move analysis. |
| .blunder | Emphasis blunders, e.g., Alert: missed double or Alert: bad move. |
| .joker | Emphasis very good or bad rolls, e.g., Alert: unlucky roll. |
| .stattable | The style applied to the entire table with game, match, and session statistics |
| .stattableheader | The header row of the statistics table |
| .result | Style for the text indicating the outcome of the game or match, e.g., Jørn Thyssen wins 16 points. |
| .tiny | Currently unused. |
| .cubedecision | The style applied to the entire cube decision table |
| .cubedecisionheader | Style for the header row of the cube decision table |
| .cubeequity | Style for any equity or MWC in the cube decision table |
| .cubeaction | Style for the text indicating the correct cube action |
| .cubeply | Style for the text that states the level of evaluation |
| .cubeprobs | Style for the game winning probabilities in the cube decision table |
| .comment | The style applied to the entire table used for annotations or comments, e.g., the kibitzing from imported SGG files |
| .commentheader | The style applied to the header row of the annotations' table |
| .number | Currently unused |
| .fontfamily | Style applied to the entire body of the XHTML document. |
| .block | Style applied to the images in the export to avoid gaps between individual pictures both horizontally and vertically. |
| .positionid | Style for the Position ID and match ID. |
GNU Backgammon (gnubg) is a program for playing and analysing backgammon positions, games and matches. It's based on a neural network. You may play GNU Backgammon using the command line or a graphical interface based on GTK+.
GNU Backgammon is mostly developed on GNU/Linux. It also builds and runs under other Unix operating systems like those derived from BSD or Solaris. The main prerequisite is the availability of the GLib library at version 2.8 or later.
Installable packages for Microsoft Windows and Mac OS X are available for download at the project official website. Already built packages are often provided by GNU/Linux distributions as well.
When you successfully port GNU Backgammon to other operating systems, you are welcome to give us a note at the GNU Backgammon mailing list.
The official website is https://www.gnu.org/software/gnubg/. Binaries and source code for GNU Backgammon can be downloaded from this site. Up to date source code can be accessed through CVS.
GNU Backgammon is Free Software and is a part of the GNU Project. You may download it for free. For more information see the GNU General Public License. But be aware that GNU Backgammon is not public domain software or shareware as you perhaps know from Microsoft Windows. GNU Backgammon is free as in freedom, i.e. all the source code is there for you to inspect, change or distribute as long as you keep said license.
Take a look at the GNU home page. It's also the page for Free Software Foundation.
A good place to start is Backgammon Galore. For an extensive link collection, go to Gammon Links.
Send an email to the GNU backgammon mailing list. If it is a bug, be sure to include the name of your operating system, the version of GNUbg you use, and any error messages you receive. Try to describe exactly what happens before the error occurs.
You're welcome! Send an email with your suggestions to the GNU backgammon mailing list.
On Microsoft Windows everything you need is included in the installer.
On Mac OS/X you will need the XQuartz Window System.
On GNU/Linux there are prerequisites as well but your package manager (apt, yum, etc...) will take care of them.
Good luck to you! Download the source code and make sure to read one of the two following two items.
Download GNU Backgammon sources as described here and follow the instructions from this document.
Details like the exact names of the prerequisite packages will vary from a distribution to another but the general process will remain identical. If you are remotely familiar with software set up with autoconf, you will see that GNU Backgammon is straightforward to build.
Check that you have installed all necessary development packages.
Look for warnings or errors during compiling. If you still don't
have a clue, send a message to
<bug-gnubg@gnu.org>.
GNU Backgammon's speed depends on the CPU only. It doesn't need much memory (any machine not totally obsolete will have enough) and does little or no I/O (a fast disk or a SSD won't make any difference).
The table below lists CPUs and the result of the command → , showing the relative speed of various processors. Note that these numbers are not directly comparable with those given by the similar command from eXtreme Gammon.
| Evals/sec | CPU | System/Main board | RAM | OS | GNUBG-Version | |
| 2378000 | Intel Xeon E5-2687W 3.00 GHz | HP Z840 | 64 GB | CentOS 7 | 1.05.002, --enable-simd=fma | 24 threads |
| 2160000 | Intel Xeon E5-2687W 3.00 GHz | HP Z840 | 64 GB | CentOS 7 | 1.05.002 | 24 threads |
| 1470000 | Intel Xeon E5-2687W 3.00 GHz | HP Z840 | 64 GB | CentOS 7 | 1.05.002 | 12 threads |
| 936000 | Intel Xeon E5-2687W 3.00 GHz | HP Z840 | 64 GB | CentOS 7 | 1.05.002 | 6 threads |
| 647000 | Intel Core i7-6670HQ 2.60 GHz | Intel NUC 6i7KYK | 16 GB | Ubuntu 16.04 | 1.05.002 | 8 threads |
| 500300 | Intel Core i7-6670HQ 2.60 GHz | Intel NUC 6i7KYK | 16 GB | Ubuntu 16.04 | 1.05.002 | 4 threads |
| 449500 | Intel Core i5-2400 3.10 GHz | Dell Optiplex 790 | 4 GB | CentOS 6 | 1.02 | 4 threads |
| 422000 | Intel Core i7-5557U 3.10 GHz | Intel NUC 5i7RYH | 8 GB | Ubuntu 16.04 | 1.05.002 | 4 threads |
| 310000 | Intel Core i7-5557U 3.10 GHz | Intel NUC 5i7RYH | 8 GB | Ubuntu 16.04 | 1.05.002 | 2 threads |
| 281000 | Intel Core i7-6670HQ 2.60 GHz | Intel NUC 6i7KYK | 16 GB | Ubuntu 16.04 | 1.05.002 | 2 threads |
| 258600 | Intel Core i5-2400 3.10 GHz | Dell Optiplex 790 | 4 GB | CentOS 6 | 1.02 | 2 threads |
| 237600 | Intel Core i5-3320M 2.60 GHz | Lenovo T430 | 4 GB | Win XP SP3 | 1.04 | 2 threads |
| 197700 | Intel Core i5-3320M 2.60 GHz | Lenovo T430 | 4 GB | Win XP SP3 | 1.02 | 2 threads |
| 182300 | Intel Xeon E5-2687W 3.00 GHz | HP Z840 | 64 GB | CentOS 7 | 1.05.002, --enable-simd=fma | 1 thread |
| 165500 | Intel Core i7-5557U 3.10 GHz | Intel NUC 5i7RYH | 8 GB | Ubuntu 16.04 | 1.05.002 | 1 thread |
| 161300 | Intel Xeon E5-2687W 3.00 GHz | HP Z840 | 64 GB | CentOS 7 | 1.05.002 | 1 thread |
| 149300 | Intel Core i7-6670HQ 2.60 GHz | Intel NUC 6i7KYK | 16 GB | Ubuntu 16.04 | 1.05.002 | 1 thread |
| 145700 | Intel Core i5-2400 3.10 GHz | Dell Optiplex 790 | 4 GB | CentOS 6 | 1.05.002 | 1 thread |
| 131400 | Intel Core i5-2400 3.10 GHz | Dell Optiplex 790 | 4 GB | CentOS 6 | 1.02 | 1 thread |
| 125100 | Intel Core 2 Duo P8400 2.26 GHz | Dell Latitude E6400 | 2 GB | Win XP SP3 | 1.02 | 2 threads |
| 119700 | Intel Core i5-3320M 2.60 GHz | Lenovo T430 | 4 GB | Win XP SP3 | 1.04 | 1 thread |
| 100100 | Intel Core i5-3320M 2.60 GHz | Lenovo T430 | 4 GB | Win XP SP3 | 1.02 | 1 thread |
| 76200 | Intel Core 2 Duo T7500 2.2 GHz | Dell Latitude D630 | 4 GB | FreeBSD 11.0 | 1.05.002 | 1 thread |
| 64300 | Intel Core 2 Duo T7500 2.2 GHz | Dell Latitude D630 | 4 GB | FreeBSD 9.2 | 1.02 | 1 thread |
| 63500 | Intel Core 2 Duo P8400 2.26 GHz | Dell Latitude E6400 | 2 GB | Win XP SP3 | 1.02 | 1 thread |
| 43700 | ARM Cortex-A53 600 MHz | Raspberry Pi 3 Model B | 1024 MB | Raspbian 9.4 | 1.06.002, --with-simd=neon | 2 threads |
| 37600 | Intel Pentium 4 2.8 GHz | Dell Optiplex GX270 | 1 GB | CentOS 5 | 1.02 | |
| 23000 | Intel Pentium 4 2.8 GHz | Asus P4P800D | 1024 MB | Win XP SP2 | 0.14.3-devel | |
| 21800 | ARM Cortex-A53 600 MHz | Raspberry Pi 3 Model B | 1024 MB | Raspbian 9.4 | 1.06.002, --with-simd=neon | 1 thread |
| 21700 | ARM Cortex-A53 600 MHz | Raspberry Pi 3 Model B | 1024 MB | Raspbian 10 | 1.06.002, --with-simd=neon | 1 thread |
| 11100 | ARM Cortex-A53 600 MHz | Raspberry Pi 3 Model B | 1024 MB | Raspbian 10 | 1.06.002 | 1 thread |
| 10400 | ARM Cortex-A53 600 MHz | Raspberry Pi 3 Model B | 1024 MB | Raspbian 9.4 | 1.05.002 | 1 thread |
| 9170 | Intel Celeron 750 MHz | Toshiba Satellite 4600 | 256 MB | Win XP SP1 | 1.04 | |
| 8520 | Intel Celeron 750 MHz | Toshiba Satellite 4600 | 256 MB | Win XP SP1 | 1.02 | |
| 6990 | Intel Celeron 600 MHz | Toshiba Satellite 4310 | 128 MB | Win XP SP2 | 1.02 |
Well, your computer wants to communicate with you. Give it a chance and read (and try to understand) what it is telling you. Then read the next items carefully:
GNU Backgammon reads several different files at start-up. It will first try to read a file called gnubg.wd. This is a file which contains all the neural net weights and is necessary for the program to evaluate positions. If this file is not found, or found corrupted or with an incompatible version, GNU Backgammon will search for a weights file called gnubg.weights. This file also contains the neural net weights, but is stored in ASCII format. If none of these files are found, GNU Backgammon will not start.
GNU Backgammon will also read the bearoff databases at start-up. There are usually two bearoff databases. The first is called gnubg_os0.bd, and has stored data about the bearoff probabilities of all position where both players have 15 or fewer checkers left on their six home board points. If this file is not found, GNU Backgammon will create a heuristic bearoff database for these positions. This database is a also called the 'One Sided Database', since it evaluates each player separately. The other bearoff database is called gnubg_ts0.bd. This bearoff database contains win probabilities for all bearoff positions with six or less checkers. It also contains cubeful equities (Money Game) for all the positions. If this file is not found at start-up, GNU Backgammon will evaluate late bearoff positions with the one sided bearoff database.
Open the Windows menu and go to the entry for GNU Backgammon. Right-click with the mouse and choose `properties'. Check, if the `working path' is the same directory as the `*.exe'-file one line above. If not, adjust the working path.
Install the newest driver for your graphic card. Be sure that you have chosen at least a desktop resolution of 65535 (16 bit color depth). If your card is a ATI Rage somewhat there still might be some problems with the graphical interface (GTK+) and Microsoft Windows.
Using Microsoft Windows, just click on the correct menu entry (`GNU Backgammon'). If it still doesn't work, check whether `C:\[path-to-your-gnubg]\gnubg.exe' exists or not.
GNU/Linux users should check if GTK+ is installed.
For GNU/Linux users: open a terminal and run gnubg -t.
Microsoft Windows™ users: Look for a file called gnubg-cli.exe in GNU Backgammon's install directory or open the Microsoft Windows menu → and type C:\[path-to-your-gnubg]\gnubg-cli.exe. There is also a menu entry GNU Backgammon CLI.
When you start a new match, you will be asked to play to a certain amount of points (for example, 7 points). The player who firstly reaches this amount wins the match. Starting a new session means playing to an infinite amount. Be aware that the rules do slightly differ, mainly the Jacoby rule is applies to sessions and the Crawford to match play.
A beaver is only allowed in a money game session. To beaver means to redouble, retaining control of the cube, immediately after your opponent doubles. For more information see the glossary at Backgammon Galore.
The easiest way to move checkers is to "drag and drop." Put your mouse pointer over a checker you want to move, press the left mouse button and drag the checker to the desired point, holding down the button while dragging.
If you prefer to use mouse clicks, the left mouse button is for the left die shown on your board. Right click your mouse for the right die.
If you always want the higher number displayed on the left, go to the menu → , click on the `Dice' tab and select Show higher die on left.
The official backgammon tournament rules allow to put up to all 15 checkers on a point. Playing with a maximum of 5 checkers, sometimes known as the Egyptian Rule, is no longer supported by GNU Backgammon.
Go to the menu → and change the values for Player 0. There is also a set of predefined settings you may choose from.
Go to the menu → and click on Player 1. At the top there is a field to change the human player's name.
Go to the menu → . Here you may change the color of checkers, the points and the board itself.
Go to the menu → and click on the `Sound' tab. Disable the option `Beep on illegal input'.
A ply describes how far GNU Backgammon evaluates the position. 0-ply means that GNU Backgammon estimates the worth of the position as it is. A 1-ply evaluation looks one step deeper, i.e. it evaluates the position after making the best possible move for each of the 21 different rolls and returns the averaged result. 2-ply is another roll further and so on.
The more plies you choose, the more you strengthen GNU Backgammon. Keep in mind that this will also decrease the playing speed.
Note also that 0-ply in GNU Backgammon is equivalent to the 1-ply evaluation of Snowie.
It's possible that Snowie's is a playing ply while gnubg's is a position evaluation ply. When playing at 1-ply Snowie will make each possible move for the player's roll (that's 1 ply) and analyse the resulting positions. Playing at 2-ply it will take each of those positions and make all the opponent moves for all possible rolls (the 2nd ply) and then analyse the resulting positions. In GNU Backgammon the initial set of possible moves is taken for granted, i.e. not counted as a ply, because gnubg's plies are position evaluation plies. Thus, for each of those possible moves a 0-ply analysis is done. gnubg's discounting of the first set of moves perhaps makes the counting seem funny.
Looking at it a different way, if you give GNU Backgammon a position and analyse it at 1-ply, it will make all the moves for all possible rolls (the 1st ply) and then analyse the resulting positions. With Snowie it will assume that the position arose from a move (that's a pretend 1st ply) then make all the moves for all possible rolls (the 2nd ply) and analyse them. This time it's Snowie that seems to be counting strangely.
You will find a small window titled `GNUbg ID' at the bottom of the GNU Backgammon window. It contains an short, textual, representation of the position at hand, suitable for easily copying and pasting positions.
It is composed of a `Position ID' describing the checkers position and a `Match ID' for the other features (match score, cube position and value, dice, who is on roll...). A detailed description of both formats is found earlier in the section called “A technical description of the Position ID”.
Pasting a `XGID' (a similar shortcut used by eXtreme Gammon) there is recognized as well.
Open a new game, match or session. If GNUbg already rolls the dice, don't bother. Press `edit', and either type the position_id and press Enter on your keyboard, or use the mouse to set up the checkers.
A mouse click at the border of the board empties the point. A left or right click sets up a certain amount of checkers depending on where exactly on the pip you click. Set up the cube with a right mouse click on it.
You can also drag and drop checkers when holding down the Ctrl key.
Finally, go to the menu and select `Game, Set turn' to choose the player on roll. The dice will then disappear.
Import of matches and positions from a number of file formats is possible: (.gam) GammonEmpire Game, (.gam) PartyGammon Game, (.mat) Jellyfish Match, (.pos) Jellyfish Position, (.sgf) Gnu Backgammon File, (.sgg) GridGammon Save Game, (.tmg) TrueMoneyGames, (.txt) Snowie Text
After analysing a game or a match GNU Backgammon is able to do some comments on checker play or cube decisions. Open the menu `Window, Game record' and you will see a list of the moves. If the actual move or cube decision differs from the best, GNU Backgammon will put a comment on it.
The default settings are:
| -0.040 | (doubtful): | ?! |
| -0.080 | (bad): | ? |
| -0.160 | (very bad): | ?? |
You may change these comment in the menu `Window, Annotation' choosing another comment for moves and/or double
GNU Backgammon determines a player's strength according to its average error (per move):
| Average Error | Skill Level |
| 0.000 .. 0.005 | Extra-terrestrial |
| 0.005 .. 0.010 | World class |
| 0.010 .. 0.015 | Expert |
| 0.015 .. 0.020 | Advanced |
| 0.020 .. 0.025 | Intermediate |
| 0.025 .. 0.030 | Beginner |
| 0.030 .. | Novice |
After analysing a game, match or session you can see the summary in the menu `Analyse, ... statistics'. Note that you can't change the ranges of these values.
The pip count is a measurement showing the total number of pips required for a player to bear off all checkers from the current position. It can be regarded as a rough estimate of the raceness of the position. A player with a lower pip count may in many situations want to try to race, whilst the opponent (with the higher pip count) may want to try blocking/holding. See also the explanation on BackGammon Galore.
(For the non-english speaking community it might be helpful to know that when you roll a six and a five, the total pips of that roll is eleven.)
When bearing off checkers, you may notice a display showing the current EPC value (next to the display of Pips). The EPC display can be turned on or off under menu Settings -> Options -> Display.
EPC stands for Effective Pip Count, and is an alternative measurement of the goodness of the position. The usual pip count can be a misleading goodness estimate when both players are bearing off. What is more important (for making cubing decisions) is the expected number of rolls each player needs to bear off hes checkers.
The effective pip count is defined as this expected number of remaining rolls, multiplied with the average number of pips in a roll, which is 8.167. (The average number of pips in a roll would be 7 if rolling a double wouldn't yield a double pip count. A double-6 yields 24 pips, not 12.)
Thus, EPC takes into account not only the current pip count, but also the expected pip wastage:
Effective Pip Count (EPC) = pip count + expected pip wastage
An example:
Position: 5 checkers on the 1-point, 4 checkers on the 2-point.
Pip count: 5x1 + 4x2 = 13
EPC: 4.41 (expected number of remaining rolls) x 8.167 = 36.02
Wasted: 36.02 - 13 = 23.02
It's clear (hopefully) that the expected pip wastage (and hence the EPC) increases with more checkers on lower points (e.g. you get pip wastage when rolling a 6 to bear off a checker from the 2- or 1-point).
It is further explained on BackGammon Galore, especially in a post by Douglas Zare.
How do one calculate the EPC then, or the expected number of remaining rolls? GNUbg uses the one-sided bearoff database, which contains the chance of bearing off the final checker in any given number of rolls. A player would probably use some quite complicated heuristics (please see the aforementioned post by Douglas Zare, and do get back here and explain it!)
In the menu `Analyse, Game/Match/Session statistics' you will see a window with some statistics. Near the bottom, you'll see four lines beginning with `Missed ... and Wrong ...'. dp means doubling point and describes a situation in the game, where you probably should have doubled your opponent.
Cash-point(CP) is your opponent's take-point now seen from your side of the board (your cash-point which equals 100% minus your opponent's take-point). GNU Backgammon uses the term missed double below cash-point, which means that the player should have doubled, and had he done so, his opponent should take. Missed double above CP in a similar way means that the correct cube-action was double pass.
If you are the leader in the match, the relevant take- and double-points will often look something like this (where TP*=CP):
The doubling windows (intervals) are:
[DP;CP] = Your doubling window! This window does not contain any information about redoubles but only the distance to the point where you do not want to play for the double amount of points.
[TP;DP] = 100% minus your opponent's doubling window now.
[reTP;reDP] = 100% minus your opponent's doubling window after he has taken.
TG is an abbreviation for too good (to double). It points to a situation in the game, where you probably should have kept the cube (mostly because of decent, sometimes very good, gammon chances) rather than double out your opponent.
Version 1.3, 3 November 2008
Copyright © 2000, 2001, 2002, 2007, 2008 Free Software Foundation, Inc.
Everyone is permitted to copy and distribute verbatim copies of this license document, but changing it is not allowed.
0. PREAMBLE
The purpose of this License is to make a manual, textbook, or other functional and useful document “free” in the sense of freedom: to assure everyone the effective freedom to copy and redistribute it, with or without modifying it, either commercially or noncommercially. Secondarily, this License preserves for the author and publisher a way to get credit for their work, while not being considered responsible for modifications made by others.
This License is a kind of “copyleft”, which means that derivative works of the document must themselves be free in the same sense. It complements the GNU General Public License, which is a copyleft license designed for free software.
We have designed this License in order to use it for manuals for free software, because free software needs free documentation: a free program should come with manuals providing the same freedoms that the software does. But this License is not limited to software manuals; it can be used for any textual work, regardless of subject matter or whether it is published as a printed book. We recommend this License principally for works whose purpose is instruction or reference.
1. APPLICABILITY AND DEFINITIONS
This License applies to any manual or other work, in any medium, that contains a notice placed by the copyright holder saying it can be distributed under the terms of this License. Such a notice grants a world-wide, royalty-free license, unlimited in duration, to use that work under the conditions stated herein. The “Document”, below, refers to any such manual or work. Any member of the public is a licensee, and is addressed as “you”. You accept the license if you copy, modify or distribute the work in a way requiring permission under copyright law.
A “Modified Version” of the Document means any work containing the Document or a portion of it, either copied verbatim, or with modifications and/or translated into another language.
A “Secondary Section” is a named appendix or a front-matter section of the Document that deals exclusively with the relationship of the publishers or authors of the Document to the Document’s overall subject (or to related matters) and contains nothing that could fall directly within that overall subject. (Thus, if the Document is in part a textbook of mathematics, a Secondary Section may not explain any mathematics.) The relationship could be a matter of historical connection with the subject or with related matters, or of legal, commercial, philosophical, ethical or political position regarding them.
The “Invariant Sections” are certain Secondary Sections whose titles are designated, as being those of Invariant Sections, in the notice that says that the Document is released under this License. If a section does not fit the above definition of Secondary then it is not allowed to be designated as Invariant. The Document may contain zero Invariant Sections. If the Document does not identify any Invariant Sections then there are none.
The “Cover Texts” are certain short passages of text that are listed, as Front-Cover Texts or Back-Cover Texts, in the notice that says that the Document is released under this License. A Front-Cover Text may be at most 5 words, and a Back-Cover Text may be at most 25 words.
A “Transparent” copy of the Document means a machine-readable copy, represented in a format whose specification is available to the general public, that is suitable for revising the document straightforwardly with generic text editors or (for images composed of pixels) generic paint programs or (for drawings) some widely available drawing editor, and that is suitable for input to text formatters or for automatic translation to a variety of formats suitable for input to text formatters. A copy made in an otherwise Transparent file format whose markup, or absence of markup, has been arranged to thwart or discourage subsequent modification by readers is not Transparent. An image format is not Transparent if used for any substantial amount of text. A copy that is not “Transparent” is called “Opaque”.
Examples of suitable formats for Transparent copies include plain ASCII without markup, Texinfo input format, LaTeX input format, SGML or XML using a publicly available DTD, and standard-conforming simple HTML, PostScript or PDF designed for human modification. Examples of transparent image formats include PNG, XCF and JPG. Opaque formats include proprietary formats that can be read and edited only by proprietary word processors, SGML or XML for which the DTD and/or processing tools are not generally available, and the machine-generated HTML, PostScript or PDF produced by some word processors for output purposes only.
The “Title Page” means, for a printed book, the title page itself, plus such following pages as are needed to hold, legibly, the material this License requires to appear in the title page. For works in formats which do not have any title page as such, “Title Page” means the text near the most prominent appearance of the work’s title, preceding the beginning of the body of the text.
The “publisher” means any person or entity that distributes copies of the Document to the public.
A section “Entitled XYZ” means a named subunit of the Document whose title either is precisely XYZ or contains XYZ in parentheses following text that translates XYZ in another language. (Here XYZ stands for a specific section name mentioned below, such as “Acknowledgements”, “Dedications”, “Endorsements”, or “History”.) To “Preserve the Title” of such a section when you modify the Document means that it remains a section “Entitled XYZ” according to this definition.
The Document may include Warranty Disclaimers next to the notice which states that this License applies to the Document. These Warranty Disclaimers are considered to be included by reference in this License, but only as regards disclaiming warranties: any other implication that these Warranty Disclaimers may have is void and has no effect on the meaning of this License.
2. VERBATIM COPYING
You may copy and distribute the Document in any medium, either commercially or noncommercially, provided that this License, the copyright notices, and the license notice saying this License applies to the Document are reproduced in all copies, and that you add no other conditions whatsoever to those of this License. You may not use technical measures to obstruct or control the reading or further copying of the copies you make or distribute. However, you may accept compensation in exchange for copies. If you distribute a large enough number of copies you must also follow the conditions in section 3.
You may also lend copies, under the same conditions stated above, and you may publicly display copies.
3. COPYING IN QUANTITY
If you publish printed copies (or copies in media that commonly have printed covers) of the Document, numbering more than 100, and the Document’s license notice requires Cover Texts, you must enclose the copies in covers that carry, clearly and legibly, all these Cover Texts: Front-Cover Texts on the front cover, and Back-Cover Texts on the back cover. Both covers must also clearly and legibly identify you as the publisher of these copies. The front cover must present the full title with all words of the title equally prominent and visible. You may add other material on the covers in addition. Copying with changes limited to the covers, as long as they preserve the title of the Document and satisfy these conditions, can be treated as verbatim copying in other respects.
If the required texts for either cover are too voluminous to fit legibly, you should put the first ones listed (as many as fit reasonably) on the actual cover, and continue the rest onto adjacent pages.
If you publish or distribute Opaque copies of the Document numbering more than 100, you must either include a machine-readable Transparent copy along with each Opaque copy, or state in or with each Opaque copy a computer-network location from which the general network-using public has access to download using public-standard network protocols a complete Transparent copy of the Document, free of added material. If you use the latter option, you must take reasonably prudent steps, when you begin distribution of Opaque copies in quantity, to ensure that this Transparent copy will remain thus accessible at the stated location until at least one year after the last time you distribute an Opaque copy (directly or through your agents or retailers) of that edition to the public.
It is requested, but not required, that you contact the authors of the Document well before redistributing any large number of copies, to give them a chance to provide you with an updated version of the Document.
4. MODIFICATIONS
You may copy and distribute a Modified Version of the Document under the conditions of sections 2 and 3 above, provided that you release the Modified Version under precisely this License, with the Modified Version filling the role of the Document, thus licensing distribution and modification of the Modified Version to whoever possesses a copy of it. In addition, you must do these things in the Modified Version:
- Use in the Title Page (and on the covers, if any) a title distinct from that of the Document, and from those of previous versions (which should, if there were any, be listed in the History section of the Document). You may use the same title as a previous version if the original publisher of that version gives permission.
- List on the Title Page, as authors, one or more persons or entities responsible for authorship of the modifications in the Modified Version, together with at least five of the principal authors of the Document (all of its principal authors, if it has fewer than five), unless they release you from this requirement.
- State on the Title page the name of the publisher of the Modified Version, as the publisher.
- Preserve all the copyright notices of the Document.
- Add an appropriate copyright notice for your modifications adjacent to the other copyright notices.
- Include, immediately after the copyright notices, a license notice giving the public permission to use the Modified Version under the terms of this License, in the form shown in the Addendum below.
- Preserve in that license notice the full lists of Invariant Sections and required Cover Texts given in the Document’s license notice.
- Include an unaltered copy of this License.
- Preserve the section Entitled “History”, Preserve its Title, and add to it an item stating at least the title, year, new authors, and publisher of the Modified Version as given on the Title Page. If there is no section Entitled “History” in the Document, create one stating the title, year, authors, and publisher of the Document as given on its Title Page, then add an item describing the Modified Version as stated in the previous sentence.
- Preserve the network location, if any, given in the Document for public access to a Transparent copy of the Document, and likewise the network locations given in the Document for previous versions it was based on. These may be placed in the “History” section. You may omit a network location for a work that was published at least four years before the Document itself, or if the original publisher of the version it refers to gives permission.
- For any section Entitled “Acknowledgements” or “Dedications”, Preserve the Title of the section, and preserve in the section all the substance and tone of each of the contributor acknowledgements and/or dedications given therein.
- Preserve all the Invariant Sections of the Document, unaltered in their text and in their titles. Section numbers or the equivalent are not considered part of the section titles.
- Delete any section Entitled “Endorsements”. Such a section may not be included in the Modified Version.
- Do not retitle any existing section to be Entitled “Endorsements” or to conflict in title with any Invariant Section.
- Preserve any Warranty Disclaimers.
If the Modified Version includes new front-matter sections or appendices that qualify as Secondary Sections and contain no material copied from the Document, you may at your option designate some or all of these sections as invariant. To do this, add their titles to the list of Invariant Sections in the Modified Version’s license notice. These titles must be distinct from any other section titles.
You may add a section Entitled “Endorsements”, provided it contains nothing but endorsements of your Modified Version by various parties — for example, statements of peer review or that the text has been approved by an organization as the authoritative definition of a standard.
You may add a passage of up to five words as a Front-Cover Text, and a passage of up to 25 words as a Back-Cover Text, to the end of the list of Cover Texts in the Modified Version. Only one passage of Front-Cover Text and one of Back-Cover Text may be added by (or through arrangements made by) any one entity. If the Document already includes a cover text for the same cover, previously added by you or by arrangement made by the same entity you are acting on behalf of, you may not add another; but you may replace the old one, on explicit permission from the previous publisher that added the old one.
The author(s) and publisher(s) of the Document do not by this License give permission to use their names for publicity for or to assert or imply endorsement of any Modified Version.
5. COMBINING DOCUMENTS
You may combine the Document with other documents released under this License, under the terms defined in section 4 above for modified versions, provided that you include in the combination all of the Invariant Sections of all of the original documents, unmodified, and list them all as Invariant Sections of your combined work in its license notice, and that you preserve all their Warranty Disclaimers.
The combined work need only contain one copy of this License, and multiple identical Invariant Sections may be replaced with a single copy. If there are multiple Invariant Sections with the same name but different contents, make the title of each such section unique by adding at the end of it, in parentheses, the name of the original author or publisher of that section if known, or else a unique number. Make the same adjustment to the section titles in the list of Invariant Sections in the license notice of the combined work.
In the combination, you must combine any sections Entitled “History” in the various original documents, forming one section Entitled “History”; likewise combine any sections Entitled “Acknowledgements”, and any sections Entitled “Dedications”. You must delete all sections Entitled “Endorsements”.
6. COLLECTIONS OF DOCUMENTS
You may make a collection consisting of the Document and other documents released under this License, and replace the individual copies of this License in the various documents with a single copy that is included in the collection, provided that you follow the rules of this License for verbatim copying of each of the documents in all other respects.
You may extract a single document from such a collection, and distribute it individually under this License, provided you insert a copy of this License into the extracted document, and follow this License in all other respects regarding verbatim copying of that document.
7. AGGREGATION WITH INDEPENDENT WORKS
A compilation of the Document or its derivatives with other separate and independent documents or works, in or on a volume of a storage or distribution medium, is called an “aggregate” if the copyright resulting from the compilation is not used to limit the legal rights of the compilation’s users beyond what the individual works permit. When the Document is included in an aggregate, this License does not apply to the other works in the aggregate which are not themselves derivative works of the Document.
If the Cover Text requirement of section 3 is applicable to these copies of the Document, then if the Document is less than one half of the entire aggregate, the Document’s Cover Texts may be placed on covers that bracket the Document within the aggregate, or the electronic equivalent of covers if the Document is in electronic form. Otherwise they must appear on printed covers that bracket the whole aggregate.
8. TRANSLATION
Translation is considered a kind of modification, so you may distribute translations of the Document under the terms of section 4. Replacing Invariant Sections with translations requires special permission from their copyright holders, but you may include translations of some or all Invariant Sections in addition to the original versions of these Invariant Sections. You may include a translation of this License, and all the license notices in the Document, and any Warranty Disclaimers, provided that you also include the original English version of this License and the original versions of those notices and disclaimers. In case of a disagreement between the translation and the original version of this License or a notice or disclaimer, the original version will prevail.
If a section in the Document is Entitled “Acknowledgements”, “Dedications”, or “History”, the requirement (section 4) to Preserve its Title (section 1) will typically require changing the actual title.
9. TERMINATION
You may not copy, modify, sublicense, or distribute the Document except as expressly provided under this License. Any attempt otherwise to copy, modify, sublicense, or distribute it is void, and will automatically terminate your rights under this License.
However, if you cease all violation of this License, then your license from a particular copyright holder is reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license, and (b) permanently, if the copyright holder fails to notify you of the violation by some reasonable means prior to 60 days after the cessation.
Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder notifies you of the violation by some reasonable means, this is the first time you have received notice of violation of this License (for any work) from that copyright holder, and you cure the violation prior to 30 days after your receipt of the notice.
Termination of your rights under this section does not terminate the licenses of parties who have received copies or rights from you under this License. If your rights have been terminated and not permanently reinstated, receipt of a copy of some or all of the same material does not give you any rights to use it.
10. FUTURE REVISIONS OF THIS LICENSE
The Free Software Foundation may publish new, revised versions of the GNU Free Documentation License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns. See https://www.gnu.org/licenses/.
Each version of the License is given a distinguishing version number. If the Document specifies that a particular numbered version of this License “or any later version” applies to it, you have the option of following the terms and conditions either of that specified version or of any later version that has been published (not as a draft) by the Free Software Foundation. If the Document does not specify a version number of this License, you may choose any version ever published (not as a draft) by the Free Software Foundation. If the Document specifies that a proxy can decide which future versions of this License can be used, that proxy’s public statement of acceptance of a version permanently authorizes you to choose that version for the Document.
11. RELICENSING
“Massive Multiauthor Collaboration Site” (or “MMC Site”) means any World Wide Web server that publishes copyrightable works and also provides prominent facilities for anybody to edit those works. A public wiki that anybody can edit is an example of such a server. A “Massive Multiauthor Collaboration” (or “MMC”) contained in the site means any set of copyrightable works thus published on the MMC site.
“CC-BY-SA” means the Creative Commons Attribution-Share Alike 3.0 license published by Creative Commons Corporation, a not-for-profit corporation with a principal place of business in San Francisco, California, as well as future copyleft versions of that license published by that same organization.
“Incorporate” means to publish or republish a Document, in whole or in part, as part of another Document.
An MMC is “eligible for relicensing” if it is licensed under this License, and if all works that were first published under this License somewhere other than this MMC, and subsequently incorporated in whole or in part into the MMC, (1) had no cover texts or invariant sections, and (2) were thus incorporated prior to November 1, 2008.
The operator of an MMC Site may republish an MMC contained in the site under CC-BY-SA on the same site at any time before August 1, 2009, provided the MMC is eligible for relicensing.
ADDENDUM: How to use this License for your documents
To use this License in a document you have written, include a copy of the License in the document and put the following copyright and license notices just after the title page:
Copyright © YEAR YOUR NAME Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.3 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled “GNU Free Documentation License”.
If you have Invariant Sections, Front-Cover Texts and Back-Cover Texts, replace the “with… Texts.” line with this:
with the Invariant Sections being LIST THEIR TITLES, with the Front-Cover Texts being LIST, and with the Back-Cover Texts being LIST.
If you have Invariant Sections without Cover Texts, or some other combination of the three, merge those two alternatives to suit the situation.
If your document contains nontrivial examples of program code, we recommend releasing these examples in parallel under your choice of free software license, such as the GNU General Public License, to permit their use in free software.
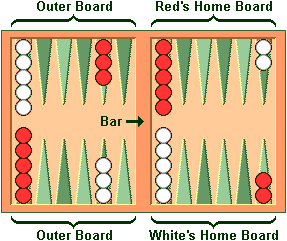
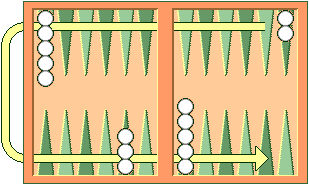
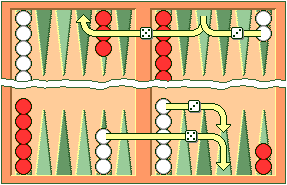
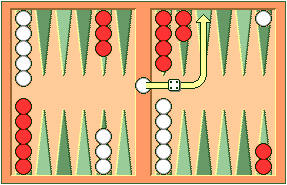
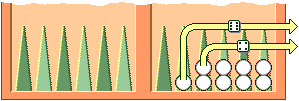
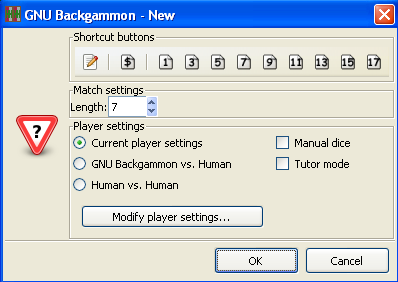
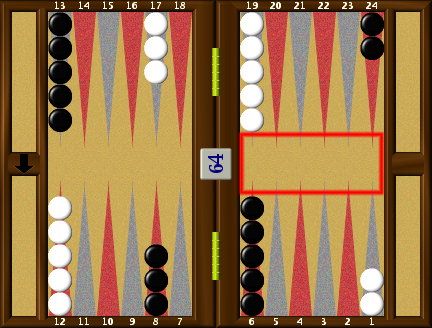
![[[cubebuttons.png]]](images/cubebuttons.png)
![[[hintwindow.png]]](images/hintwindow.png)
![[[hintcubewindow.png]]](images/hintcubewindow.png)
![[[tutor.png]]](images/tutor.png)
![[[tutorwarning.png]]](images/tutorwarning.png)
![[[clearboard.png]]](images/clearboard.png)
![[[initialboard.png]]](images/initialboard.png)
![[[analysesettings.png]]](images/analysesettings.png)
![[[gamerecord.png]]](images/gamerecord.png)
![[[analasyepane.png]]](images/analysepane.png)
![[[evalsettings.png]]](images/evalsetting.png)
![[[movefilterex.png]]](images/movefilterex.png)
![[[movefilter1.png]]](images/movefilter1.png)
![[[movefilter2.png]]](images/movefilter2.png)
![[[movefilter3.png]]](images/movefilter3.png)
![[[cubeful-ex1.png]]](images/cubeful-ex1.png)
![[[cubeful-ex2.png]]](images/cubeful-ex2.png)
![[[appearance.png]]](images/appearence.png)
![[[cubefuleq-ex1.png]]](images/cubefuleq-ex1.png)
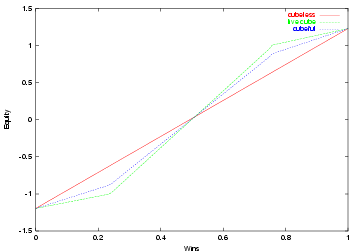
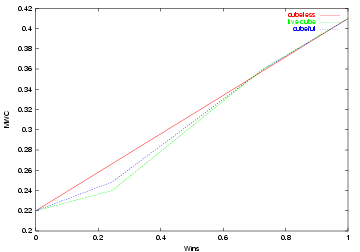
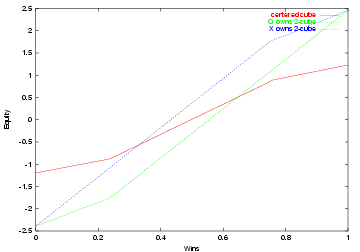
![[[doubleline.png]]](images/doubleline.png)