4.6.1 Symétrie centrale

Résultat mathématique. Cette transformation est définie par un point O appelé centre de la symétrie. Déplacer une figure par une symétrie de centre O, c’est faire tourner cette figure d’un demi-tour autour du point O. La symétrie centrale est une isométrie : la figure et sa transformée ont la même forme et les mêmes dimensions, les figures sont superposables.

Dans l’Exemple 4.17 ci-dessous, le triangle est transformé par la symétrie de centre O(-1;-1).

| figure triangle o |
figure := DrGeoFigure nouveau.
o := figure point: -1 @ -1.
triangle := figure polygone: { 0@0. 3@4. 5@2 }.
figure symétriqueDe: triangle selonCentre: o

Maintenant s’entraîner avec l’exercice suivant.

4.6.2 Symétrie axiale

Résultat mathématique. Cette transformation est définie par une droite d appelée axe de la symétrie. En pliant la feuille suivant le droite d, la figure et sa transformée se superposent. Cette transformation est également une isométrie.

Dans l’Exemple 4.18 ci-dessous, le triangle est transformé par la symétrie d’axe la droite d passant par les points (-3;0) et (5;-5).

| figure triangle d |
figure := DrGeoFigure nouveau.
d := figure droitePassantPar: -3 @ 0 et: 5 @ -5.
triangle := figure polygone: { 0@0. 3@4. 5@2 }.
figure symétriqueDe: triangle selonAxe: d

Maintenant s’entraîner avec l’exercice suivant.

4.6.3 Translation

Résultat mathématique. Cette transformation est définie par un vecteur v appelé vecteur de translation. Déplacer une figure par une translation, c’est faire glisser cette figure selon la direction, le sens et la longueur du vecteur v, sans la faire tourner. Cette transformation est une isométrie.

Dans l’Exemple 4.19 ci-dessous, le triangle est translaté selon le vecteur v d’origine le point A(1;1) et d’extrémité B(6;5).

| figure triangle a b v |
figure := DrGeoFigure nouveau.
a := figure point: 1 @ 1.
b := figure point: 6 @ 5.
v := figure vecteurOrigine: a extrémité: b.
triangle := figure polygone: { 1@3. 3@7. 5@5 }.
figure translationDe: triangle parVecteur: v

Maintenant s’entraîner avec l’exercice suivant.

4.6.4 Rotation

Résultat mathématique. Cette transformation est définie par un point O appelé centre de la rotation, et un angle a appelé angle de la rotation. Déplacer une figure par une rotation de centre O et d’angle a, c’est faire tourner cette figure autour du point O d’un angle de a. La mesure de l’angle a est positive ou négative – sens contraire des aiguilles d’une montre (sens anti-horaire) ou sens des aiguilles d’une montre (sens horaire).

L’exemple ci-dessous montre les rotations d’un triangle avec une mesure d’angle positive puis une mesure d’angle négative.

| figure triangle o a1 a2 |
figure := DrGeoFigure nouveau.
o := figure point: 1 @ 1.
a1 := 70 degreesToRadians.
a2 := -70 degreesToRadians.
triangle := figure polygone: { 1@3. 3@7. 5@5 }.
figure rotationDe: triangle parCentre: o etAngle: a1.
figure rotationDe: triangle parCentre: o etAngle: a2

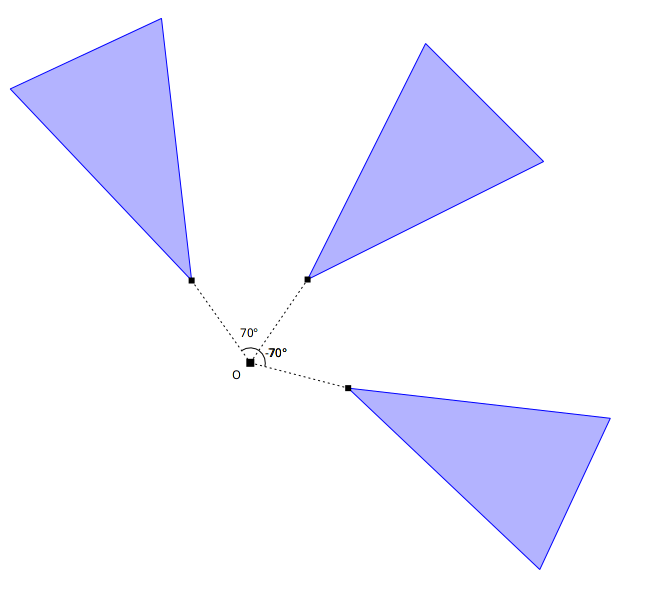
Figure 4.21: Deux rotations avec des angles de 70° et -70°

Maintenant s’entraîner avec l’exercice suivant.

4.6.5 Homothétie

Résultat mathématique. Cette transformation géométrique est définie par un point O appelé centre de l’homothétie, et une valeur numérique k appelée rapport de l’homothétie. Elle agrandit ou réduit proportionnellement une figure selon le rapport k
Lorsque le rapport k est entre -1 et 1, la figure transformée est réduite.
Cette transformation n’est pas une isométrie, elle ne conserve par les longueurs.

| figure triangle o k1 k2 |
figure := DrGeoFigure nouveau.
o := figure point: 8 @ 7.
k1 := 1/4.
k2 := -1/3.
triangle := figure polygone: { 1@3. 3@7. 5@5 }.
(figure homothétieDe: triangle parCentre: o etFacteur: k1)
   nommer: Réduite et dans le même sens'.
(figure homothétieDe: triangle parCentre: o etFacteur: k2)
   nommer: 'Réduite et inversée'

Lorsque le rapport k est supérieur à 1 ou inférieur à -1, la figure est agrandie par rapport à la figure originale.

| figure triangle o k1 k2 |
figure := DrGeoFigure nouveau.
o := figure point: 8 @ 7.
k1 := 3.
k2 := -2.
triangle := figure polygone: { 1@3. 3@7. 5@5 }.
(figure homothétieDe: triangle parCentre: o etFacteur: k1)
   nommer: 'Agrandie et dans le même sens'.
(figure homothétieDe: triangle parCentre: o etFacteur: k2)
   nommer: 'Agrandie et inversée'

Maintenant s’entraîner avec l’exercice suivant.

4.6.6 Transformer une collection d’objets

Dans les exemples et les exercices précédents nous transformions des objets simples tels que des triangles et des carrés. Parfois nous souhaitons transformer un groupe d’objets, par exemple un carré avec un cercle inscrit à l’intérieur comme dans l’Exercice 2.12. L’exemple suivant montre qu’il est possible de transformer un à un les quatre côtés du segment et le cercle.

| figure c1 c2 c3 c4 cercle d |
figure := DrGeoFigure nouveau.
c1 := figure segmentDe: -2 @ 2 à: 2 @ 2.
c2 := figure segmentDe: 2 @ 2 à: 2 @ -2.
c3 := figure segmentDe: 2 @ -2 à: -2 @ -2.
c4 := figure segmentDe: -2 @ -2 à: -2 @ 2.
cercle := figure cercleCentre: 0 @ 0 rayon: 2.
d := figure droitePassantPar: -7 @ 0 et: 0 @ -8.
figure symétriqueDe: c1 selonAxe: d.
figure symétriqueDe: c2 selonAxe: d.
figure symétriqueDe: c3 selonAxe: d.
figure symétriqueDe: c4 selonAxe: d.
figure symétriqueDe: cercle selonAxe: d

Nous remarquons que les 5 dernières lignes du code sont quasiment identiques. Cela indique souvent que ce code peut-être modifié afin d’être moins répétitif. Une première chose que nous pouvons faire c’est de grouper toutes les parties de notre figure (les 4 côtés du carré et le cercle) dans une collection d’objet. Dans le langage Smalltalk il existe des objets de type Collection pour y mettre toutes sortes d’objets comme des constructions géométriques.

Nous avons déjà rencontré des collections de type tableau avec le code figure polygone: { 1@0. 5@0. 5@4 . 1@4 }. Dans cet exemple, une collection avec 4 objets de type coordonnées de points est créé. A la place de ces coordonnées nous pouvons placer les 5 parties géométriques de notre figure à transformer – les côtés du carré et le cercle inscrit à l’intérieur. Observer alors dans l’Exemple 4.23 ci-dessous comment le code a été réécrit.

| figure collection d |
figure := DrGeoFigure nouveau.
d := figure droitePassantPar: -7 @ 0 et: 0 @ -8.
collection := {figure segmentDe: -2 @ 2 à: 2 @ 2 .
   figure segmentDe: 2 @ 2 à: 2 @ -2 .
   figure segmentDe: 2 @ -2 à: -2 @ -2 .
   figure segmentDe: -2 @ -2 à: -2 @ 2 .
   figure cercleCentre: 0 @ 0 rayon: 2}.
collection faire: [:forme | figure symétriqueDe: forme selonAxe: d]

Lors de la création de la collection, les instructions pour créer les parties constituantes de la figure sont séparées par des “.”. Ensuite l’envoi du message faire: à cette collection crée le symétrique de chacune de ses formes. Le nombre de lignes du code source du programme est ainsi presque divisé par 2.

Faire les exercices suivants pour s’entraîner.

Observer les deux figures ci-dessous pour comprendre avec quels segments, cercles et polygone elles sont construites :

Figure 4.22: Spirale

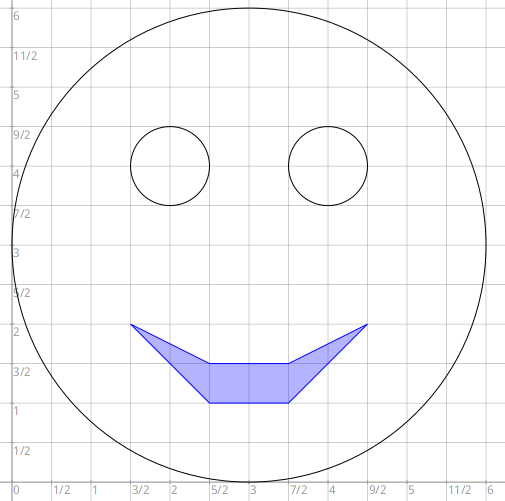
Figure 4.23: Smiley

Pour Résumer. Placer des objets géométriques dans une collection permet d’appliquer alors une transformation sur chacun de ces objets. Le code informatique écrit est alors plus court, cela s’appelle parcourir une collection pour y faire un traitement informatique – ici appliquer une transformation géométrique. Cette pratique est très importante en programmation.

4.6.7 Transformations en cascade

Pour prolonger l’étude précédente, il serait intéressant d’appliquer à nouveau une transformation géométrique sur les objets déjà transformés. Recopier le code de l’Exemple 4.25.

| figure collection v |
figure := DrGeoFigure nouveau.
v := figure vecteur: 2 @ 0.
collection := {figure segmentDe: 0 @ 0 à: 1 @ 3.
   figure segmentDe: 1 @ 3 à: 1 @ 3.
   figure segmentDe: 1 @ 3 à: 2 @ 0}.
5 foisRepete: [ 
   collection := collection collecter: [ :forme |
      figure translationDe: forme parVecteur:  v ] ]

Dans cet exemple, deux boucles imbriquées – l’une dans l’autre – sont utilisées. La première boucle est foisRepete:, ici elle répète 5 fois son bloc de code en paramètre. Dans le bloc de code de cette première boucle se trouve la deuxième boucle collecter:.

Comme avec le message faire:, collecter: translate chacun des objets de la collection mais, en plus, il collecte ces objets translatés dans une nouvelle collection. Celle-ci est ensuite affectée à la variable collection. Enfin la boucle foisRepete: est reprise et répétée encore quatre fois.

Voici un autre exemple au code plus complexe mais plus intéressant esthétiquement.

| figure collection d1 d2 d3 d4 d5|
figure := DrGeoFigure nouveau.
d1 := (figure droitePassantPar: 4@0 et: 4@5) pointillé.
d2 := (figure droitePassantPar: 1@0 et: 1@5) pointillé.
d3 := (figure droitePassantPar: -2@0 et: -2@5) pointillé.
d4 := (figure droitePassantPar: -5@0 et: -5@5) pointillé.
d5 := (figure droitePassantPar: -8@0 et: -8@5) pointillé.
collection := {(figure segmentDe: 7@1 à: 4@1) normal.
   (figure segmentDe: 4@1 à: 4@4) normal.
   (figure segmentDe: 4@4 à: 7@4) normal.
   (figure segmentDe: 7@4 à: 7@2) normal.
   (figure segmentDe: 7@2 à: 5@2) normal.
   (figure segmentDe: 5@2 à: 5@3) normal.
   (figure segmentDe: 5@3 à: 6@3) normal}.
{d1 . d2 . d3 . d4 . d5} faire: [:axe |
   collection := collection collecter: [:forme |
      figure symétriqueDe: forme selonAxe: axe] ]

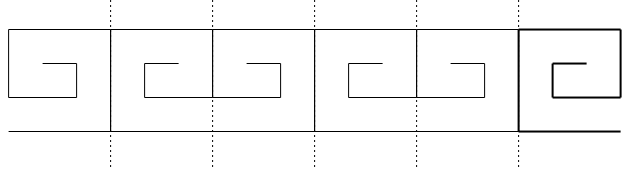
Figure 4.24: Frise de spirales

Ce code est plus technique, il utilise deux collections : une collection de droites {d1 . d2 . d3 . d4 . d5}, puis le message collecter: pour rassembler les objets transformés par les symétries axiales dans une nouvelle collection. Cette collection est alors affectée à la variable collection.

Une telle figure où un motif géométrique est transformé horizontalement à plusieurs reprises s’appelle une frise. Les symétries, translation et rotation sont utilisées pour produire des frises à partir d’un motif de base.