4.7.1 Translation

La frise ci-dessous montre un motif déplacé successivement deux fois par une translation de vecteur v. Noter que le motif lui-même n’admet pas d’axe de symétrie.

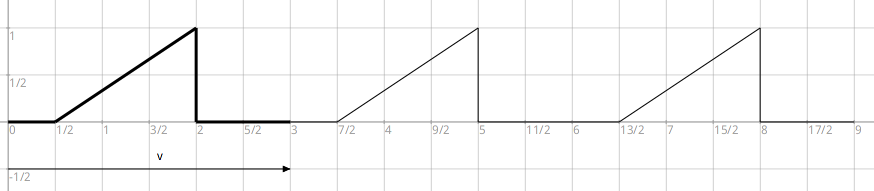
Figure 4.25: Une frise par une translation

À partir de ce motif de base, il est maintenant possible de construire une frise. Pour ce faire, le motif est glissé horizontalement de 3 unités vers la droite ou la gauche, c’est en fait la largeur du motif. Le motif est répété 5 fois à l’aide d’une boucle avec le message foisRepete:.

Voici un autre exemple avec une frise plus élaborée telle que rencontrée dans les rues de l’île de Rhodes Grecque.

Figure 4.26: Frise vue dans une rue de Rhodes (galets de plage)

Cette frise est construite à partir d’un motif élémentaire répété horizontalement à l’aide d’une transformation géométrique, ici une translation. Ce motif élémentaire est une représentation symbolique des vagues de la mer, après tout Rhodes est une île Grecque de la méditerranée.

Figure 4.27: Mise en évidence du motif élémentaire d’une frise

Maintenant que le motif de base est codé et groupé dans une collection, il est possible de construire une frise. Pour ce faire, le motif est glissé horizontalement de 4 unités vers la droite ou la gauche, c’est en fait la largeur du motif (adapter selon la largeur du motif créé par chacun à l’Exercice 4.53).

Ce glissement est une transformation géométrique : une translation de vecteur v(4;0) par exemple.

Dans la frise résultante, il est intéressant de mettre en évidence le motif de base.

Voici une autre frise construite à partir d’une spirale au tracé plus élaboré.

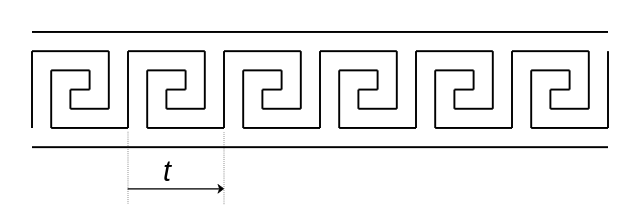
Figure 4.28: Encore une spirale

Pour construire cette frise, nous utilisons la translation. Dans la section suivante nous montrons que d’autres transformations géométriques sont utilisables pour construire une frise

4.7.2 Symétrie axiale

Observer la frise ci-dessous. Elle est construite par la translation de vecteur v du motif dessiné en trait épais.

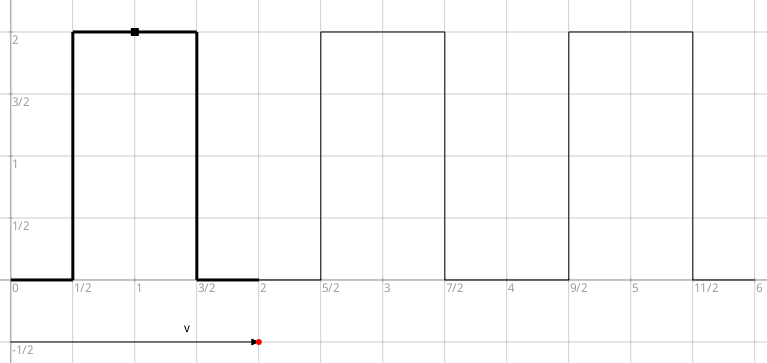
Figure 4.29: Une frise par translation mais...

Toutefois le motif admet un axe de symétrie comme montré dans la figure ci-dessous. Cela signifie que le motif de base de la frise se simplifie en un motif élémentaire composé d’uniquement 3 segments.

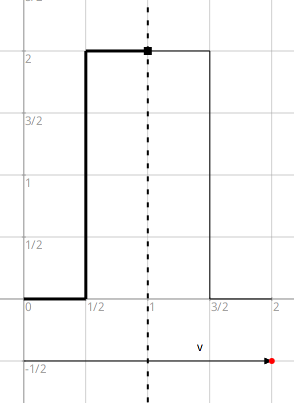
Figure 4.30: ...aussi une symétrie axiale

Maintenant pour construire la frise, nous procédons en deux étapes avec deux transformations :

1. Une symétrie axiale pour compléter le motif élémentaire et obtenir le motif complet tel que montré dans la Figure 4.30. L’axe de la symétrie passe par les points (1;0) et (1;3).
2. Une translation de vecteur v pour déplacer le motif complété et construire l’ensemble de la frise montrée dans Figure 4.29

Aussi à l’étape 1, le symétrique du motif élémentaire doit être ajouté à la collection du motif. Cela se fait avec un code informatique nouveau, nous montrons comment le faire dans l’exemple ci-dessous.

| figure collection symétriques axe |
figure := DrGeoFigure nouveau.
axe := figure droitePassantPar: 1@0 et: 1@3.
collection := {figure segmentDe: 0@0 à: (1/2)@0.
   figure segmentDe: (1/2)@0 à: (1/2)@2.
   figure segmentDe: (1/2)@2 à: 1@2} commeCollectionOrdonnée.
symétriques := collection collecter: [:forme |
   figure symétriqueDe: forme selonAxe: axe].
collection ajouterTout: symétriques

Il y a deux nouveaux messages dans ce code informatique.

• Le message unaire commeCollectionOrdonnée envoyé à la collection créée avec le motif élémentaire. Ce message transforme la collection en une collection ordonnée où il est possible d’y ajouter des objets ultérieurement.
• Le message à mot clé ajouterTout: pour ajouter le contenue d’une collection à une autre. Ici les segments symétriques sont ajoutés à la collection du motif élémentaire. Après l’envoi de ce message, collection contient 6 segments et non plus 3 comme initialement.

4.7.3 Symétrie centrale

Voici une frise qui se construit à partir d’un motif élémentaire qui est un losange – couleur foncée dans la figure ci-dessous. Ce motif est ensuite complété à l’aide d’une symétrie centrale. Puis, à l’aide d’une translation de vecteur V, la frise est construite dans son ensemble.

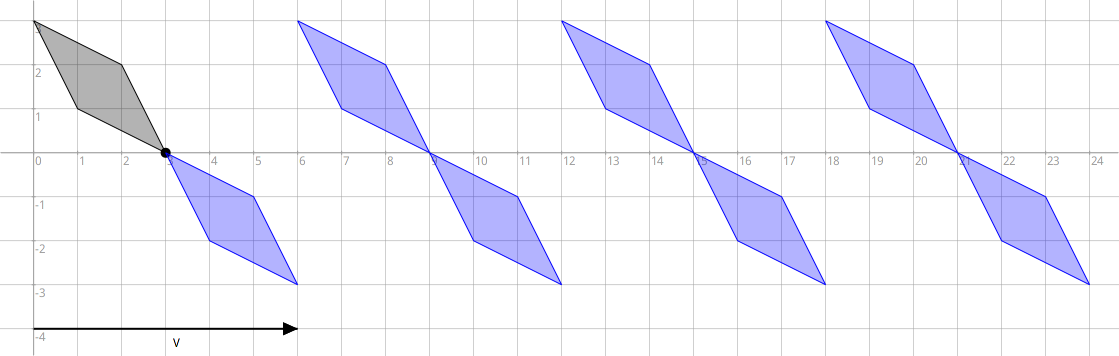
Figure 4.31: Frise et symétrie

4.7.4 Symétrie centrale et symétrie axiale

Voici une autre frise dont le motif élémentaire est toujours un losange – nommé Motif 1 dans la figure ci-dessous. Ce motif est complété par une symétrie centrale comme dans l’exemple précédent, cela donne Motif 2. Ensuite, et c’est nouveau, une symétrie axiale d’axe la droite d est utilisée : Motif 1 se transforme en Motif 3 et Motif 2 se transforme en Motif 4.

L’utilisation de la symétrie centrale puis de la symétrie axiale nous donne ce motif en forme d’étoile. Il est alors translaté autant de fois que souhaité pour obtenir une frise.

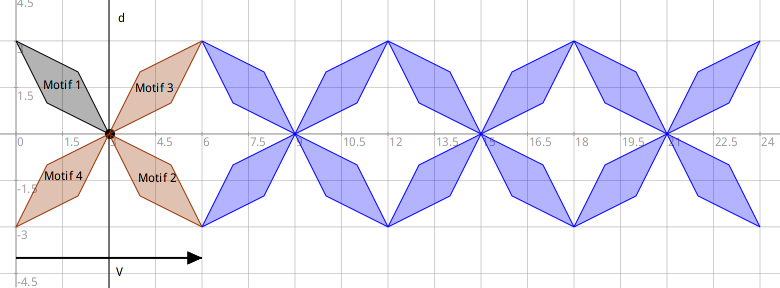
Figure 4.32: Frise et symétries

Ce chapitre sur les frises géométriques est maintenant terminé. Il est possible d’en inventer et programmer beaucoup d’autres. Avec un peu d’observation, tu découvriras d’autres frises dans les monuments architecturaux, historiques ou récents.