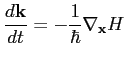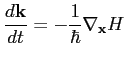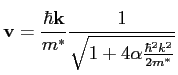The Drift Process

As seen previously, an electron moving in a crystal lattice moves just like a free electron, but with a change of mass. This fact justify us to use the classical equations of motion, in order to describe the motion of electrons and holes in a semiconductor device. We can, thus, use the Hamilton formalism to get the electron equations of motion. They read as follow

$$\frac{d \bf {x}}{dt} = \frac{1}{\hbar} \nabla_{\bf {k}} H$$ (5.10)

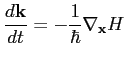$$\frac{d \bf {k}}{dt} = -\frac{1}{\hbar} \nabla_{\bf {x}} H$$ (5.11)

where 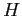$H$ is the Hamiltonian of the system, i.e.

$$H = {\cal{E}}(\bf {k}) + V(\bf {x})$$

Then, if we use the Kane dispersion relation, we get, after some simple algebra, the following expression for the electron velocity

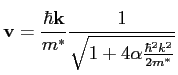$${\bf {v}} = \frac{\hbar {\bf {k}}}{m^*} \frac{1}{\sqrt{1 + 4 \alpha \frac{\hbar^2 k^2}{2 m^*}}}$$ (5.12)